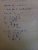finding the maximum and minimum of trigonometry curves. (1 Viewer)

[girlworld_club]

i am having trouble with this concept in general because instead of differentiating to find dy/dx then equating to zero (then solving normally), the answer in the book draw the graph instead and look on the max and min points on there. Why do they do this?

i.e this question.

between 5am and 5pm on march 2009, the height, h, of the tide in a harbour is given by:

h = 1 + 0.7sin(pie/2)t for 0<t<12

where h is metres and t is hours, with t=0 at 5am.

i) What was the value of h at low tide, and at what time did low tide occur.

ii) also i am having problems algebraically solving:

1.35 = 1 + 0.7sin(pie/2)t to find t

could someone explain? Thanks

 

[girlworld_club]

However in other questions they differentiate to find maximum and minimum points e.g

find the maximum and minimum values of 1 + root3sinx + coxs in the interval O<x<2(pie)

 

[Menomaths]

Is this something else or simple algebraic manipulation?
1.35 = 1 + 0.7sin(pie/2)t
0.35 = 0.7t
t= 1/2?

 

[girlworld_club]

the answers are pie/6 and 5(pie)/6

 

[HeroicPandas]

'pie'?

 

[girlworld_club]

i meant pi, opps. must of been very hungry. can anyone help me out?

 

[girlworld_club]

P.s are two unit student required to know the formulae a cos x + b sin x = R cos(x − α) (i haven't encountered it in my book) but it would help to solve for some max and min functions.

 

[anthony_wheels]

I'm pretty sure it's right... If I'm wrong, someone please correct me

 

[girlworld_club]

in the very first line, i am curious why you you times the sin (pi/4) by t and brought the t in the bracket. Can you do that?

 

[anthony_wheels]

Well, that's what I assumed the question meant. As sin(pi/2) is a constant i.e. 1. So if the t wasn't inside the brackets then the height of the water increase monotonically (keep on increasing as the time increases), which we know isn't possible because the tides increase and decrease.

 

[anthony_wheels]

Also, is it pi/2 or pi/4, because your original post says pi/2?

 

[HeroicPandas]

P.s are two unit student required to know the formula a cos x + b sin x = R cos(x − α) (i haven't encountered it in my book) but it would help to solve for some max and min functions.

no thats 3U

 

[girlworld_club]

can you give me the specifics of why you did each line like that.