Halp. Linear Algebra (1 Viewer)

[Riproot]

View attachment 25439

What the fuck even is 1cii??

 

[qwerty44]

invalid attachment

 

[Riproot]

cn!!!Jajajdkadianxishai

 

[Fus Ro Dah]

View attachment 25440cn!!!Jajajdkadianxishai

Translation:

"Two lines pass through P_0 and Q_0, and are parallel to v and w respectively. Find the shortest distance between the two lines".

Recall that the shortest distance between a point P and another line containing point Q and also in the same direction as v, since there are infinite lines going through a single point, is given by the following formula:



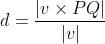
where PQ is the vector whose length we want to find.

To do this question:

1. Pick a random point on the vector passing through Q and in the direction of v.
2. Observe that v has ijk expression v=4i+j-k.
3. By simple calculation, find the equation of the vector PQ.
4. Substitute all the information you have into the formula. This will of course involve computation of the Cross Product.

Alternatively, you could do the following:

1. Realise that the equivalent length d is the modulus of the vector component of PR, where R is some point lying on the vector passing through Q in the direction of v, orthogonal to the vector v.
2. Use the formula for orthogonal vector components to compute the modulus of the vector PR.
3. Use Pythagoras' Theorem to find the distance between the two points and hence the minimal distance between the two lines. We do this because the vector of minimal modulus passing through the lines going through P and Q, is orthogonal to both vectors.

 

[Riproot]

Only read the translation. I will read the rest if I get stuck. Thanks bby.

 

[NWO]

lol is that maths in uni.? if yes gg lol