KingOfActing
lukewarm mess
Yeah. Well that's hard. But jokes aside, do you know that the Riemann Zeta function WAS actually examined in the HSC in 1975? So here is a not-so-hard question - HSC 1975 4 unit Q9i:
See if you can do it.
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Yeah. Well that's hard. But jokes aside, do you know that the Riemann Zeta function WAS actually examined in the HSC in 1975? So here is a not-so-hard question - HSC 1975 4 unit Q9i:
See if you can do it.
Your way works, just evaluate the integral:The infinite sum is a first-order linear approximation of the following integral:
Two approximations are constructed such that they are definitively greater and lesser than the true value of the integral. Since the integral only converges for s>1, it follows that the sum only converges for s>1. QED.
This isn't a formal proof, strictly speaking, but I cbbs rn. I'll come back to patch it up later.
Bumpand also this one about counting technique:
How many whole numbers from 1000 to 9999 have 6 as the sum of their digits?
Nice.
Let D(a,b) be the number of ways to make a sum of a with b numbers.Bump
It is obvious none of the digits can be greater than 6.and also this one about counting technique:
How many whole numbers from 1000 to 9999 have 6 as the sum of their digits?
Since the sum of the digits must be 6, we can write it as:and also this one about counting technique:
How many whole numbers from 1000 to 9999 have 6 as the sum of their digits?
Although the idea is good, I think the answer is not that, since multiple bars can exist next to each otherSince the sum of the digits must be 6, we can write it as:
1_1_1_1_1_1_
Just use the stars and bars method, since we need to put in 3 bars to represent the digits. So we get
i.e. 1_1 | 1_1 | 1 | 1 = 2211
56 is also what I got.Since the sum of the digits must be 6, we can write it as:
1_1_1_1_1_1_
Just use the stars and bars method, since we need to put in 3 bars to represent the digits. So we get
i.e. 1_1 | 1_1 | 1 | 1 = 2211
tywebb's site has a proof of Fermat's Theorem. I don't quite get it. But it is still fascinating.I have discovered a truly marvellous proof of this, which this post is too small to contain.
Quite a lot of background is needed to understand Wiles' proof at any greater depth than the absolute "top level overview".tywebb's site has a proof of Fermat's Theorem. I don't quite get it. But it is still fascinating.
My method allows for that (56 is most definitely correct).Although the idea is good, I think the answer is not that, since multiple bars can exist next to each other
OP is a Year 12 student Extension 1. These are not in the scope of the HSC syllabus.1. By considering the cross-sections of the figure, sketch
2. Ifshow that
Note I am using older notation here (edit here is the equivalent notation)

Well, it is clear z > 0. By setting z to 1 (or any other positive constant), it's clear that the horizontal cross-section is that of an ellipse, which is stretched with major axis being the y-axis. By considering y or x being constant, it is clear the shape traced is that of a parabola. Hence the shape is an "elliptic paraboloid" (is that the right term?). Basically it's like a 3-d parabola that's stretched on the y-axis.1. By considering the cross-sections of the figure, sketch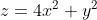
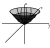
wow thats actually pree impressive paint skills lolWell, it is clear z > 0. By setting z to 1 (or any other positive constant), it's clear that the horizontal cross-section is that of an ellipse, which is stretched with major axis being the y-axis. By considering y or x being constant, it is clear the shape traced is that of a parabola. Hence the shape is an "elliptic paraboloid" (is that the right term?). Basically it's like a 3-d parabola that's stretched on the y-axis.
masterful paint skills View attachment 33073
thanks manwow thats actually pree impressive paint skills lol
would rep but
"You must spread some Reputation around before giving it to KingOfActing again."
Nice Question
Trivial by inspection.Here's a funny one from Fort Street Leaving Certificate trial 1959 Question 3a:
Differentiate xxx
