Hermes1
Banned
- Joined
- Oct 4, 2010
- Messages
- 1,282
- Gender
- Male
- HSC
- 2011
it is given that for three positive real numbers a, b and c,
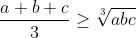
if we also no that a+b+c = 1, prove that:
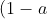(1-b)(1-c)\geq 8abc)
new to inequalities, would someone be able to help me wiff this question.
and earlier in the question i proved:
 - i dont no if this is relevant to above question.
- i dont no if this is relevant to above question.
if we also no that a+b+c = 1, prove that:
new to inequalities, would someone be able to help me wiff this question.
and earlier in the question i proved:
Last edited:
