With the circle geometry question, for ii;
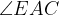
(
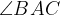
) is a fixed angle as it lies on the fixed chord BC.
Therefore in triangle AEC,
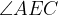
and
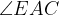
are constants, thus
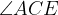
is a constant angle.
Since the constant angle
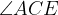
(
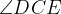
) subtends the chord ED on the circle BCDE, then ED is a constant length.
for iii;
Let M be the midpoint of ED and L the midpoint of BC, and consturct ML and EL.
EM=MD ( M is the midpoint of ED)
therefore EM=1/2ED ( a constant value)
Also EL is a constant value as it is the radius of the circle BCDE.
ML is perpendicular to ED ( perpendicular line from the centre of the circle BCDE bisects the chord ED)
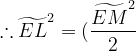+\widetilde{ML}^{2})
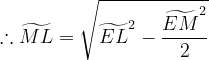
(a constant value, as EL and EM are constants)
Since ML is a constant, it is the radius of the locus M which lies on the circle with the with centre L.