I need full working out  Or else I'll end up not getting it again ><" Thanks!
Or else I'll end up not getting it again ><" Thanks!
1)Simplify
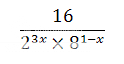
2) A country property increased in value by 12.5% to a new value of $36 000. What was the value of the property before the increase?
3)

4)

5)

6)

7)

8)

a)

b)

Please help D:
1)Simplify
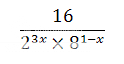
2) A country property increased in value by 12.5% to a new value of $36 000. What was the value of the property before the increase?
3)

4)

5)

6)

7)

8)

a)

b)

Please help D:
