I'll take a look at it tomorrow when I have time.
That would be greatly appreciated, thank you.
==============
However I decided to tackle the problem from a different point, and I decided to change the limit of integration of alpha to 0, to alpha to pi/2. It has given some interesting results:
\theta \ d \theta = \int_{\pi/2}^{\alpha} \frac{\sin 2n\theta}{2\sin \theta} \ d\theta )
Now we will integrate the LHS, we end up with:
\alpha}{2k-1} - \sum_{k=1}^{n} \frac{(-1)^{k+1}}{2k-1} = \int_{\pi/2}^{\alpha} \frac{\sin 2n \theta}{2\sin \theta} \ d\theta )
Then integrate once more with the limits that I already had then take n off to infinity, I end up with something very perculiar:
^2} - \pi \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{2k-1} = \lim_{n \to \infty} \int_{0}^{\pi} \left( \int_{\pi/2}^{\alpha} \frac{\sin 2n \theta}{2\sin \theta} \ d\theta \right) d\alpha )
Now, if you can notice the second term on the left hand side is pi/4 (this can proved in various ways, as shown on the first page and otherwise). And you can notice a multiplier of pi to pi/4 making pi^2/4...
This means that IF we can prove that the RHS = 0. Everything falls into place very nicely here.
That:
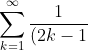^2} = \frac{\pi^2}{8} )
===========
Now when trying to prove the RHS is zero, if I integrate by parts once, I get two terms the first term has a multiplier of 1/2n on the front
and the integral that we get also has a co-efficient of 1/2n at the front. Am I allowed to then assume that since n goes to infinity the terms converge to zero despite the fact that we have an uncounted definite integral?
If you integrate by parts you get:
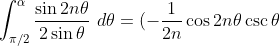|_{\pi/2}^{\alpha} - \frac{1}{2n} \int_{\pi/2}^{\alpha} \frac{\cos 2n\theta \cos \theta}{\sin^2 \theta} \ d\theta )
Can I then say this all converges to zero due to the 1/2n as n approaches infinity?


