Help: Perms and combs (1 Viewer)
- Thread starter leehuan
- Start date
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Hint: For every choice of three cards, there exists exactly one permutation where the numbers are descending.
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,650
- Gender
- Undisclosed
- HSC
- 2015
Is the answer 1/4Can't find the trick.

Simply 1/3! = 1/6.Is the answer 1/4
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Wow. Golden. Thanks.Hint: For every choice of three cards, there exists exactly one permutation where the numbers are descending.
Or, given any hand, there's 3! = 6 ways to order them, and exactly one is in descending order, so 1/6.Wow. Golden. Thanks.
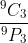
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Yep that makes sense too. I completely overlooked that only one option out of 6 is in descending order.Or, given any hand, there's 3! = 6 ways to order them, and exactly one is in descending order, so 1/6.
rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
Do you know the answer? I'm getting 5860.
Last edited:
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
I got 549 but I'm not confident with this. nevermind, it's definitely wrong if 0 can be the first number
I got 670 including 0 as first number
I got 670 including 0 as first number
Last edited:
rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
Oh, well here's what I did:
Case 1: 4 unique numbers (1234)
10*9*8*7 = 5040. 10 numbers for the first (0-9), 9 for the second (0-9 excluding the first number) etc.
Case 2: 2 unique numbers (1123)
10*1*9*8 = 720
Case 3: 1 unique numbers (1112)
10*1*1*9 = 90
Case 4: 0 unique numbers (1111)
10*1*1*1 = 10
In total: 5040 + 720 + 90 + 10 = 5860 combinations.
Edit: Didn't know 0 could be the first number. Fixed now.
Case 1: 4 unique numbers (1234)
10*9*8*7 = 5040. 10 numbers for the first (0-9), 9 for the second (0-9 excluding the first number) etc.
Case 2: 2 unique numbers (1123)
10*1*9*8 = 720
Case 3: 1 unique numbers (1112)
10*1*1*9 = 90
Case 4: 0 unique numbers (1111)
10*1*1*1 = 10
In total: 5040 + 720 + 90 + 10 = 5860 combinations.
Edit: Didn't know 0 could be the first number. Fixed now.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Hm, so if 0 can be the first number would you just replace 9->10, 8->9 and 7->8?Oh, well here's what I did:
Case 1: 4 unique numbers (1234)
9*9*8*7 = 4536. 9 numbers for the first (1-9, assuming 0123 is not a 4 digit number), 9 for the second (0-9 excluding the first number) etc.
Case 2: 2 unique numbers (1123)
9*1*8*7 = 504
Case 3: 1 unique numbers (1112)
9*1*1*8 = 72
Case 4: 0 unique numbers (1111)
9*1*1*1 = 9
In total: 4536 + 504 + 72 + 9 = 5121 combinations.
And 2 x 2 unique numbers what about those?
rand_althor
Active Member
- Joined
- May 16, 2015
- Messages
- 554
- Gender
- Male
- HSC
- 2015
Yep I changed it.Hm, so if 0 can be the first number would you just replace 9->10, 8->9 and 7->8?
And 2 x 2 unique numbers what about those?
My bad, didnt consider that case:
Case 5: 2 pairs of unique numbers (1122)
10*1*9*1 = 90
Total ways = 5860 + 90 = 5950 combinations.
Zlatman
Member
- Joined
- Nov 4, 2014
- Messages
- 73
- Gender
- Male
- HSC
- 2015
I got 715, I think the 5950 accounts for the order of the number, which we don't need to worry about.
No repeated numbers: 10C4 = 210 (pick any 4 from the 10)
2 unique numbers: 9C2 x 10 = 360 (pick one from the 10 to have 2 digits, then pick 2 from the remaining 9)
1 unique number: 10 x 9 = 90 (pick one from the 10 to have 3 digits, then pick one of the remaining 9)
No unique number: 10 = 10 (pick one of the 10 to have 4 digits)
Two pairs of repeated numbers: 10C2 = 45 (pick two of the 10 to have 2 digits)
Total numbers = 715
No repeated numbers: 10C4 = 210 (pick any 4 from the 10)
2 unique numbers: 9C2 x 10 = 360 (pick one from the 10 to have 2 digits, then pick 2 from the remaining 9)
1 unique number: 10 x 9 = 90 (pick one from the 10 to have 3 digits, then pick one of the remaining 9)
No unique number: 10 = 10 (pick one of the 10 to have 4 digits)
Two pairs of repeated numbers: 10C2 = 45 (pick two of the 10 to have 2 digits)
Total numbers = 715
Last edited:
Just going to post my next question in this original thread..
________________________________________________
My friend gave me this question and I'm stumped again.
Oh and 0 can be the first number.
Last edited:
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,805
- Gender
- Male
- HSC
- 2015
Would not have thought about using stars and bars for this. That interpretation is correct. But how come it doesn't agree with Ziatman?
Zlatman
Member
- Joined
- Nov 4, 2014
- Messages
- 73
- Gender
- Male
- HSC
- 2015
My answer was wrong, but I fixed it. For the last case, I assumed there was order (which I was correcting rand for, lol).Would not have thought about using stars and bars for this. That interpretation is correct. But how come it doesn't agree with Ziatman?
