I'm having some trouble getting the answer for question 7b.
View attachment 34901View attachment 34902
Let me ask you a question, what do you know if
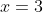
is a double root of the equation?
If that is the case then you can have
^{2})
is a root of the equation.
Now you have this in the net we can now have
\left(...\right))
What do we have here?
We want
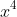
as the leading pronumeral so now we will have
\left(x^{2}\pm{...}\right))
Next, you have to take into account that you have
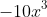
We already have from the previous step
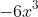
so how do we get
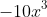
. Take away
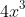
.
As such we have
\left(x^{2}-4x\pm{...}\right))
To make your life easier instead of going for the x squared term or the x term we are finding the constant.
So in this case 9 times what gives 9. The answer is simply 1.
There we have
\left(x^{2}-4x+1\right))
Now you can do whatever you want with
)
to find the factors and as such it will give you the answer that you have shown us.