goobi
Member
- Joined
- Oct 6, 2010
- Messages
- 196
- Gender
- Male
- HSC
- 2012
This question is from Ex. 3.2 of Terry Lee's textbook.
Factorise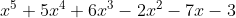 as real factors, given that it has a repeated zero.
as real factors, given that it has a repeated zero.
The suggested solution is:
=x^5+5x^4+6x^3-2x^2-7x-3)
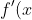=5x^4+20%20x^3+18%20x^2-4%20x-7)
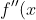%20=%2020%20x^3+60%20x^2+36%20x-4)
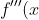%20=%2060x^2+120%20x%20+36)
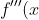%20=%2012%20(5%20x^2+10%20x+3))
As f'''(x) has no real linear factors, we must find the multiple root from f''(x).
(^This is the part that I don't understand. When we factorise f'''(x), we get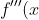=12(x-\frac{-(5+\sqrt{10})}{5})(x-\frac{-(5-\sqrt{10})}{5})) which are actually real and linear factors despite not being rational.)
which are actually real and linear factors despite not being rational.)
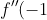=0)
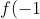=0)
Therefore, (x+1) is the triple root.
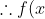=x^5+5x^4+6x^3-2x^2-7x-3)
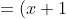^3(x^2+2x-3))
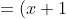^3(x+3)(x-1))
The solution is undoubtedly correct, but I still don't understand the bold part.
Any help would be greatly appreciated
Factorise
The suggested solution is:
As f'''(x) has no real linear factors, we must find the multiple root from f''(x).
(^This is the part that I don't understand. When we factorise f'''(x), we get
Therefore, (x+1) is the triple root.
The solution is undoubtedly correct, but I still don't understand the bold part.
Any help would be greatly appreciated
Last edited:
