I don't know what approach they seek, but my approach (potentially going beyond year 9 or 10 Maths*) is as follows:
Rearranging the given equation to make

the subject, I get that
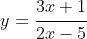
and sketching this gives a rectangular hyperbola with asymptotes at
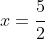
and
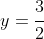
.
View attachment 32730
From this graph, a few things are immediately clear:
- as
 increases,
increases,  decreases
decreases
- we can only have both
 and
and  for
for 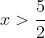 and hence the minimum possible value for
and hence the minimum possible value for  is 3.
is 3.
- as
 increases,
increases,  approaches the value 1.5, and so I can find an upper bound for
approaches the value 1.5, and so I can find an upper bound for  by examining the case
by examining the case 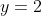 :
:
 \qquad \text{provided $x \ne \cfrac{5}{2}$, so we don't multiply by 0} \\ 3x + 1 &= 4x - 10 \\ 1 + 10 &= 4x - 3x \\ x &= 11 \end{align*})
- So, if
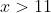 then
then 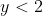 (as
(as  decreases when
decreases when  increases), and since
increases), and since  is bounded below by 1.5 for positive
is bounded below by 1.5 for positive  ,
,  cannot be an integer if
cannot be an integer if 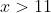 . In other words, all solutions must satisfy
. In other words, all solutions must satisfy 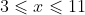 .
.
- We already have one solution,
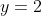 and
and 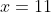 , for which
, for which 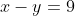
We could now find all solutions by trial-and-error by sequentially testing
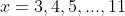
. This gives us that
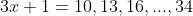
and that
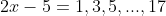
, and thus
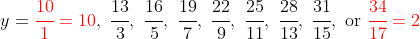
So, there are two solutions:
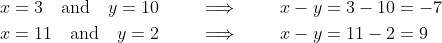
If the requirement that

and

be positive is removed, but they are still required to be integers, two other solutions appear:
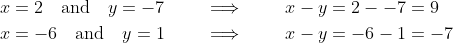
but it does not add any extra possible values for
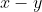
, which can only be -7 or 9.
* A note on "potentially going beyond year 9 or 10 Maths"... I originally defined a function
 = x - y= x - \cfrac{3x+1}{2x-5})
which has an oblique asymptote of
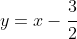
and then used the fact that
)
must be an integer to constrain the possible domain of

... once
)
is sufficiently close to the asymptote, any integer value of

will give a non-integer value of
)
. As I was typing this up, however, I realised that I could simplify the method by looking at just the above hyperbola, which makes the level of the Maths involved suited to junior high school so long as hyperbolas have been covered.


