Help (1 Viewer)

eternallyboreduser · Feb 16, 2024

Stuck on the 16a and 17, pls help. Thanks

its_ace21 · Feb 16, 2024

are u at school rn

eternallyboreduser · Feb 16, 2024

its_ace21 said:
are u at school rn

yes

Luukas.2 · Feb 16, 2024

For Q16(a)...

$\text{Suppose $A = 1$. Then, at the common root $x = \alpha$, $g(\alpha) = \alpha^2 + \alpha + 1 = 0$ . . . (*)}$

$\begin{align*} \text{Hence,} \quad f(\alpha) = \alpha^3 + \alpha^2 + \alpha + B &= 0 \\ \alpha\left(\alpha^2 + \alpha + 1\right) + B &= 0 \\ \alpha \times 0 + B &= 0 \qquad \text{on substituting (*)} \\ B &= 0 \end{align*}$

Thus, if $A = 1$ , to follows that $B = 0$ ... but the question states that $B \neq 0$ , and so it is not possible for $A = 1$ , and thus $A \neq 1$ .

Luukas.2 · Feb 16, 2024

To start, for Q 17...

Put x = p / q into the second equation given and eliminate fractions. You should get that $ap^3 - 3pq^2 + bq^3 = 0$ where a, b, p, and q are all integers. Expressing this as $ap^3 = 3pq^2 - bq^3 = q^2(3p - bq)$ , what can we deduce about a, recalling that p and q share no common factors other than 1 and -1? Use the same approach for the other result. Then, consider what this means for the original equation (*).

Luukas.2 · Feb 25, 2024

I was asked to expand on my comments with a more detailed answer, so here goes:

Part (a)

$\begin{align*} x^3 - 3x - 1 &= 0 \qquad \qquad \text{. . . . . (*)} \\ \\ \text{Let $x = \frac{p}{q}$, where $p$ and $q$ are coprime and $pq \neq 0$, be a root of} \qquad ax^3 - 3x + b &= 0 \qquad \text{where $a$, $b \in \mathbb{Z}$} \\ a\left(\frac{p}{q}\right)^3 - 3\left(\frac{p}{q}\right) + b &= 0 \\ \frac{ap^3}{q^3} - \frac{3p}{q} + b &= 0 \\ ap^3 - 3pq^2 + bq^3 &= 0 \\ \\ \text{This statement may be expressed as} \qquad ap^3 &= 3pq^2 - bq^3 = q^2(3p - bq) \quad \quad \text{. . . . . (1)} \\ \text{Or, alternatively, as} \qquad bq^3 &= 3pq^2 - ap^3 = p(3q^2 - ap^2) \quad \quad \text{. . . . . (2)} \end{align*}$

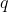
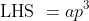
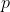
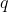
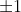
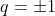
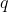
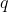
Now, $q$ is clearly a factor of the RHS of statement (1), and so must also be a factor of $\text{LHS}\ = ap^3$ . However, with $p$ and $q$ being coprime (and so sharing no factors other than $\pm 1$ , it follows that either $q = \pm 1$ or $q$ is a factor of $a$ . In either case, $q$ divides $a$ .

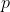
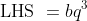
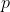
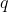
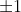
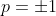
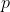
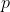
Similarly, $p$ is clearly a factor of the RHS of statement (2), and so must also be a factor of $\text{LHS}\ = bq^3$ . However, with $p$ and $q$ being coprime (and so sharing no factors other than $\pm 1$ , it follows that either $p = \pm 1$ or $p$ is a factor of $b$ . In either case, $p$ divides $b$ .

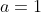
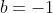
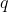
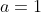
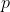
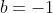
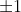
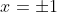
The equation (*) is the same equation with $a = 1$ and $b = -1$ . For this equation to have a rational root requires $q$ divides $a = 1$ and $p$ divides $b = -1$ or that they are $\pm 1$ . In other words, the only possible rational roots of (*) are $x = \pm 1$ . However:

$\begin{align*} \text{Test $x = 1$ in (*):} \qquad \text{LHS} &= x^3 - 3x - 1 = 1^3 - 3(1) - 1 = 1 - 3 - 1 = -3 \neq 0 \qquad \implies \qquad x = 1\ \text{is not a root of (*)} \\ \text{Test $x = -1$ in (*):} \qquad \text{LHS} &= x^3 - 3x - 1 = (-1)^3 - 3(-1) - 1 = -1 + 3 - 1 = 1 \neq 0 \quad \implies \quad x = -1\ \text{is not a root of (*)} \end{align*}$

Hence, the equation (*) has no rational roots.

Part (b)

$\begin{align*} \text{Let $x = r + s\sqrt{d}$ be a root of (*):} \qquad \left(r + s\sqrt{d}\right)^3 - 3\left(r + s\sqrt{d}\right) - 1 &= 0 \qquad \text{where $r$, $s$, and $d \in \mathbb{Q}$ but $\sqrt{d} \notin \mathbb{Q}$} \\ r^3 + 3r^2s\sqrt{d} + 3r\left(s\sqrt{d}\right)^2 + \left(s\sqrt{d}\right)^3 -3r - 3s\sqrt{d} - 1 &= 0 \\ r^3 + 3r^2s\sqrt{d} + 3rs^2d + s^3d\sqrt{d} - 3r - 3s\sqrt{d} - 1 &= 0 \\ \left(r^3 + 3rs^2d - 3r - 1\right) + s\sqrt{d}\left(3r^2 + s^2d - 3\right) &= 0 \\ \text{Since $\sqrt{d} \notin \mathbb{Q}$ and thus $d \neq 0$, this can only be true if} \qquad s\sqrt{d}\left(3r^2 + s^2d - 3\right) &= 0 \\ 3r^2s + s^3d - 3s &= 0 \qquad \text{as required} \end{align*}$

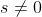
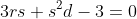
In fact, since $s \neq 0$ (as that would make the root being tested rational, which is impossible from part (a)), we have actually shown that $3rs + s^2d - 3 = 0$ , and also that $r^3 + 3rs^2d - 3r - 1 = 0$ .

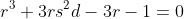
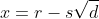
Testing $x = r - s\sqrt{d}$ will yield $\text{LHS} = \left(r^3 + 3rs^2d - 3r - 1\right) - s\sqrt{d}\left(3r^2 + s^2d - 3\right) = 0$ using these results, confirming that it must also be a root.

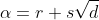
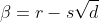
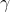
Knowing that two of the roots are $\alpha = r + s\sqrt{d}$ and $\beta = r - s\sqrt{d}$ and setting the third root to $\gamma$ , it follows that

$\begin{align*} \alpha + \beta + \gamma &= -\frac{0}{1} \\ \left(r + s\sqrt{d}\right) + \left(r - s\sqrt{d}\right) + \gamma &= 0 \\ \gamma = -2r \end{align*}$

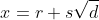
but this makes the third root rational, which is impossible by part (a), and so there can be no root of the form $x = r + s\sqrt{d}$ .

eternallyboreduser · Feb 25, 2024

How do yk this? @Luukas.2

Screenshot_20240225_212746_Samsung Internet.jpg

Luukas.2 · Feb 25, 2024

eternallyboreduser said:
How do yk this? @Luukas.2View attachment 42589

I showed that $\left(r^3 + 3rs^2d - 3r - 1\right) + s\sqrt{d}\left(3r^2 + s^2d - 3\right) = 0.$

Recognise that this expression is the sum of a rational and an irrational term, and yet is also zero...

$\begin{align*} \text{Let} \qquad \left(r^3 + 3rs^2d - 3r - 1\right) + s\sqrt{d}\left(3r^2 + s^2d - 3\right) &\equiv A + B\sqrt{d} \quad \text{where $A, B \in \mathbb{Q}$} \qquad \qquad \text{. . . . . (**)} \\ \\ \text{Since $\sqrt{d} \notin \mathbb{Q}$ but $r,\ s,\ d \in \mathbb{Q}$:} \qquad B\sqrt{d} &= s\sqrt{d}\left(3r^2 + s^2d - 3\right) \qquad \text{on equating irrational parts in (**)} \\ \text{And:} \qquad \qquad A &= r^3 + 3rs^2d - 3r - 1 \qquad \text{on equating rational parts in (**)} \\ \\ \text{Now, as $\sqrt{d} \notin \mathbb{Q}$} \qquad A + B\sqrt{d} &= 0 \quad \implies \quad B = 0 \quad \text{as $\sqrt{d} \neq 0$ and $\sqrt{d} \neq -\frac{A}{B} \in \mathbb{Q}$} \\ s\left(3r^2 + s^2d - 3\right) &= 0 \\ 3r^2 + s^2d - 3 &= 0 \quad \text{as $s \neq 0$} \\ \\ \text{Putting this result into (**):} \qquad A + s\sqrt{d} \times 0 &= 0 \\ A &= 0 \\ r^3 + 3rs^2d - 3r - 1 &= 0 \end{align*}$

Help (1 Viewer)

eternallyboreduser

Well-Known Member

its_ace21

/æɪs/

eternallyboreduser

Well-Known Member

Luukas.2

Well-Known Member

Luukas.2

Well-Known Member

Luukas.2

Well-Known Member

eternallyboreduser

Well-Known Member

Luukas.2

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)