Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Higher Level Integration Marathon & Questions (2 Viewers)
- Thread starter leehuan
- Start date
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Evaluate:
^2}{k^2})
Evaluate:
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Hint: Parseval's Theorem
Hint: Parseval's Theorem
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Evaluate:
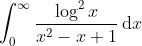
Hence, or otherwise, evaluate:
}} \right)} \, \text{d}\theta)
Evaluate:
Hence, or otherwise, evaluate:
Paradoxica
-insert title here-
Last edited:
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
Paradoxica
-insert title here-
Nice stack exchange steal.
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 463
- Gender
- Undisclosed
- HSC
- 2015
Haha was redirected there by someone after I couldn't answer it for themNice stack exchange steal.
Paradoxica
-insert title here-
Observe that the term
This observation leads us to the immediate conclusion:
Cases must be taken for the sign of log(a²)
For log(a²)<0:
For log(a²)>0:
Proof is left as an exercise to the reader.
Last edited:
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
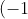^n \zeta{(n+1)} \Gamma{(n)})
Similarly, the answer to the second integral is:
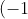^{n-1} \eta{(n+1)} \Gamma{(n)})
These come from the integral definitions of the Riemann Zeta and Dirichlet Eta functions, respectively, with slight manipulation.
By inspection, the answer to the first integral is:
Similarly, the answer to the second integral is:
These come from the integral definitions of the Riemann Zeta and Dirichlet Eta functions, respectively, with slight manipulation.
Paradoxica
-insert title here-
The answer to this integral is:
Some methods to try: DUTIS, Contour Integration
Re: Extracurricular Integration Marathon
Can you please show working out? I can't really learn from this and what is this "slight manipulation" that you have stated.By inspection, the answer to the first integral is:
Similarly, the answer to the second integral is:
These come from the integral definitions of the Riemann Zeta and Dirichlet Eta functions, respectively, with slight manipulation.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
} \equiv \frac{2}{\pi}\sum_{k=1}^\infty \frac{(2\mathcal{H}_{2k} - \mathcal{H}_k)\sin{kx}}{k})
Then by Parseval's Theorem:
}\text{d}x = \frac{4}{\pi^2} \sum_{k=1}^\infty \left(\frac{2\mathcal{H}_{2k} - \mathcal{H}_k}{k}\right)^2)
The integral evaluates to π³/2, so the sum is π⁴/8
The function to consider is:Evaluate:
^2}{k^2})
Then by Parseval's Theorem:
The integral evaluates to π³/2, so the sum is π⁴/8
Last edited:
Re: Extracurricular Integration Marathon
. (b) is done in a similar fashion.$)
$ and the gamma function $\Gamma (z)$. These are:$)
 = \sum^\infty_{n = 1} \frac{1}{n^s}$ and $\Gamma (z) = \int^\infty_0 e^{-x} x^{z - 1} \, dx.)
$, which is$)
 = - \sum^\infty_{k = 1} \frac{x^k}{k}, \qquad -1 < x \leq 1.)
 we have$)
 [\ln x]^{n - 1} \frac{dx}{x} = -\sum^\infty_{k = 1} \int^1_0 \frac{x^k}{k} [\ln x]^{n - 1} \frac{dx}{x}\end{align*})

^n \sum^\infty_{k = 1} \int^\infty_0 e^{-ku} u^{n - 1} \, du.\end{align*})

^n \sum^\infty_{k = 1} \frac{1}{k^{n + 1}} \int^\infty_0 e^{-t} t^{n - 1} \, dt = (-1)^n \zeta (n + 1) \Gamma (n),\end{align*})


Can you please show working out? I can't really learn from this and what is this "slight manipulation" that you have stated.
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
the first one is a trivial exercise in contour integration/special functions manipulation
the second is a matter of a straightforward substitution
anyway let's bump this one, been sitting here for a very long time.Evaluate:
Hence, or otherwise, evaluate:
}} \right)} \, \text{d}\theta)
the first one is a trivial exercise in contour integration/special functions manipulation
the second is a matter of a straightforward substitution
Paradoxica
-insert title here-
Re: Extracurricular Integration Marathon
Beta Function manipulation is pretty trivial....
Re: Extracurricular Integration Marathon

Beta function, second derivative with respect to its parameter to get rid of the log squared term, beta function reflection formula is then related to the digamma function (and of course its second derivatives will be needed along the way), then a reflection formula for the digamma function and I guess we are home and hosed but is it not nice to see something differentBeta Function manipulation is pretty trivial....

