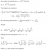Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
Yes you are correct, apologies.Just checking - should there be a proviso that cos alpha is not equal to +/- 1 ?