HSC 2012-14 MX2 Integration Marathon (archive) (2 Viewers)

Trebla · Sep 5, 2012

Re: MX2 Integration Marathon

In that case, something more hardcore

$$Suppose that $I_n=\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx \\\\\\$(a)\quad Show that $I_{n+2}\leq I_{n+1} \leq I_{n}\\\\$(b)\quad Show that $I_{n+2}=\dfrac{n+1}{n+2}I_n\\\\$(c)\quad Hence show that as $\dfrac{I_{n+1}}{I_n}\rightarrow1$ as $n\rightarrow\infty\\\\$(d)\quad Using (b), deduce that $I_{2n}=\dfrac{(2n-1)\times(2n-3)\times...\times3\times1}{2n\times(2n-2)\times...\times4\times2\times1}.\dfrac{\pi}{2}$

$\!\!\!\!\!\!\!\!\!$(e)\quad Prove by mathematical induction that for integers $n\geq0$\\\\ $I_{2n+1}=\dfrac{2n\times(2n-2)\times...\times4\times2}{(2n+1)\times(2n-1)\times...\times5\times3\times1}\\\\$(f)\quad One application of this reduction formula is by relating it to a well known result called Stirling's formula which approximates $n!$. Suppose that for some positive constant $R\\\\ n!=R\sqrt{n}\left(\dfrac{n}{e}\right)^n\\\\$Using the results of (c), (d) and (e), show that as $n\rightarrow\infty$ then $R\rightarrow\sqrt{2\pi}$

barbernator · Sep 5, 2012

Re: MX2 Integration Marathon

TheProfessional said:
$\int e^{e^{x}+x}dx=\int e^{e^{x}}+e^{x}dx$
Let $u=e^{x}$
$\int e^{u}+e^{x}\frac{du}{e^{x}}=e^{e^{x}}+c$

u got the correct answer with the wrong working.

TheProfessional · Sep 5, 2012

Re: MX2 Integration Marathon

barbernator said:
u got the correct answer with the wrong working.

I had a plus instead of times lol
will fix it.

barbernator · Sep 5, 2012

Re: MX2 Integration Marathon

<a href="http://www.codecogs.com/eqnedit.php?latex=a)~within~the~domain~0\leq x\leq \frac{\pi }{2},~~ 0\leq sinx\leq 1\\ Taking~sinx\leq 1,~sin^{n@plus;1}x\leq sin^{n}x\\ \therefore \int_{0}^{\frac{\pi }{2}}sin^{n@plus;1}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n}x\\ hence,~it~follows~that~ \int_{0}^{\frac{\pi }{2}}sin^{n@plus;2}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n@plus;1}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n}x~as~required" target="_blank"><img src="http://latex.codecogs.com/gif.latex?a)~within~the~domain~0\leq x\leq \frac{\pi }{2},~~ 0\leq sinx\leq 1\\ Taking~sinx\leq 1,~sin^{n+1}x\leq sin^{n}x\\ \therefore \int_{0}^{\frac{\pi }{2}}sin^{n+1}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n}x\\ hence,~it~follows~that~ \int_{0}^{\frac{\pi }{2}}sin^{n+2}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n+1}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n}x~as~required" title="a)~within~the~domain~0\leq x\leq \frac{\pi }{2},~~ 0\leq sinx\leq 1\\ Taking~sinx\leq 1,~sin^{n+1}x\leq sin^{n}x\\ \therefore \int_{0}^{\frac{\pi }{2}}sin^{n+1}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n}x\\ hence,~it~follows~that~ \int_{0}^{\frac{\pi }{2}}sin^{n+2}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n+1}x\leq \int_{0}^{\frac{\pi }{2}}sin^{n}x~as~required" /></a>

<a href="http://www.codecogs.com/eqnedit.php?latex=b)~let~v=sin^{n-1}x~~~u=-cosx\\\\ dv=(n-1)cosxsin^{n-2}xdx~~~du=sinx\\\\ I_{n}=-cosxsin^{n-1}x]^\frac{\pi }{2}_{0}@plus;(n-1)\int_{\frac{\pi }{2}}^{0}cos^{2}xsin^{n-2}xdx\\\\ I_{n}=(n-1)\int_{\frac{\pi }{2}}^{0}(1-sin^{2}x)sin^{n-2}xdx\\\\ I_{n}=(n-1)I_{n-2}-(n-1)I_{n}\\\\ nI_{n}=(n-1)I_{n-2}~whoops~it~asked~for~n@plus;2~:/\\\\ I_{n}=\frac{n-1}{n}I_{n-2}\\\\ let~n=k@plus;2\\\\ I_{n@plus;2}=\frac{n@plus;1}{n@plus;2}I_{n}~QED" target="_blank"><img src="http://latex.codecogs.com/gif.latex?b)~let~v=sin^{n-1}x~~~u=-cosx\\\\ dv=(n-1)cosxsin^{n-2}xdx~~~du=sinx\\\\ I_{n}=-cosxsin^{n-1}x]^\frac{\pi }{2}_{0}+(n-1)\int_{\frac{\pi }{2}}^{0}cos^{2}xsin^{n-2}xdx\\\\ I_{n}=(n-1)\int_{\frac{\pi }{2}}^{0}(1-sin^{2}x)sin^{n-2}xdx\\\\ I_{n}=(n-1)I_{n-2}-(n-1)I_{n}\\\\ nI_{n}=(n-1)I_{n-2}~whoops~it~asked~for~n+2~:/\\\\ I_{n}=\frac{n-1}{n}I_{n-2}\\\\ let~n=k+2\\\\ I_{n+2}=\frac{n+1}{n+2}I_{n}~QED" title="b)~let~v=sin^{n-1}x~~~u=-cosx\\\\ dv=(n-1)cosxsin^{n-2}xdx~~~du=sinx\\\\ I_{n}=-cosxsin^{n-1}x]^\frac{\pi }{2}_{0}+(n-1)\int_{\frac{\pi }{2}}^{0}cos^{2}xsin^{n-2}xdx\\\\ I_{n}=(n-1)\int_{\frac{\pi }{2}}^{0}(1-sin^{2}x)sin^{n-2}xdx\\\\ I_{n}=(n-1)I_{n-2}-(n-1)I_{n}\\\\ nI_{n}=(n-1)I_{n-2}~whoops~it~asked~for~n+2~:/\\\\ I_{n}=\frac{n-1}{n}I_{n-2}\\\\ let~n=k+2\\\\ I_{n+2}=\frac{n+1}{n+2}I_{n}~QED" /></a>

nightweaver066 · Sep 5, 2012

Re: MX2 Integration Marathon

$I_n = \int ^{\pi /2}_0 sin^nxdx$

$= -\int ^{\pi /2}_0 sin^{n - 1}x d(cosx)$

$= -[sin^{n - 1}xcosx]^{\pi /2}_0 + \int ^{\pi /2}_0 (n - 1)sin^{n - 2}cos^2xdx$

$= (n - 1) \int^{\pi /2}_0 sin^{n - 2}(1 - sin^2x}dx$

$= (n - 1) \int ^{\pi /2}_0 sin^{n-2}xdx - (n - 1)\int^{\pi /2}_0 sin^nxdx$

$= (n - 1)I_{n - 2} - (n - 1)I_n$

$\therefore nI_n = (n - 1)I_{n - 2}$

$I_n = \frac{n - 1}{n}I_{n - 2}$

$Replacing (n) with (n + 2)$

$I_{n + 2} = \frac{n + 1}{n + 2}I_n$

$\frac{I_{n + 2}}{I_n} = \frac{n + 1}{n + 2}$

$$As $ n \rightarrow \infty, \; \frac{n + 1}{n + 2} \approx \frac{n}{n} = 1$

$\therefore \frac{I_{n + 2}}{I_n} \rightarrow 1 \; as \; n \rightarrow \infty$

$I_{2n} = \frac{2n - 1}{2n}I_{2n - 2}$

$= \frac{2n - 1}{2n} \times \frac{2n - 3}{2n - 2}I_{2n - 4}$

$...$

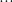
$= \frac{(2n - 1) \times (2n - 3) \times (2n - 5) \times ... \times 3 \times 1}{(2n) \times (2n - 2) \times (2n - 4) \times ... \times 2} \times I_0$

$I_0 = \int ^{\pi /2}_0 dx$

$= [x]^{\pi /2}_0$

$= \pi /2$

$\therefore I_{2n} = \frac{(2n - 1) \times (2n - 3) \times (2n - 5) \times ... \times 3 \times 1}{(2n) \times (2n - 2) \times (2n - 4) \times ... \times 2 \times 1} \times \frac{\pi}{2}$

cutemouse · Sep 5, 2012

Re: MX2 Integration Marathon

Trebla said:
In that case, something more hardcore

$$Suppose that $I_n=\displaystyle\int_0^{\frac{\pi}{2}}\sin^nx\,dx \\\\\\$(a)\quad Show that $I_{n+2}\leq I_{n+1} \leq I_{n}\\\\$(b)\quad Show that $I_{n+2}=\dfrac{n+1}{n+2}I_n\\\\$(c)\quad Hence show that as $\dfrac{I_{n+1}}{I_n}\rightarrow1$ as $n\rightarrow\infty\\\\$(d)\quad Using (b), deduce that $I_{2n}=\dfrac{(2n-1)\times(2n-3)\times...\times3\times1}{2n\times(2n-2)\times...\times4\times2\times1}.\dfrac{\pi}{2}$

$\!\!\!\!\!\!\!\!\!$(e)\quad Prove by mathematical induction that for integers $n\geq0$\\\\ $I_{2n+1}=\dfrac{2n\times(2n-2)\times...\times4\times2}{(2n+1)\times(2n-1)\times...\times5\times3\times1}\\\\$(f)\quad One application of this reduction formula is by relating it to a well known result called Stirling's formula which approximates $n!$. Suppose that for some positive constant $R\\\\ n!=R\sqrt{n}\left(\dfrac{n}{e}\right)^n\\\\$Using the results of (c), (d) and (e), show that as $n\rightarrow\infty$ then $R\rightarrow\sqrt{2\pi}$

Lol, wallis product... nice

Sindivyn · Sep 5, 2012

Re: MX2 Integration Marathon

asianese said:
I'm not sure about this bit

Let A = sinx
=1/2 * root (1+k^2)
Make a substitution of tanC
= 1/2 * integration of sec^3 x
Integration by parts and done ( don't forget to sub EVERYTHING back in )

is that the same x as before? If so you went in a huge circle. Where did a k come from?? (I'm actually confused - trying to work it out)

Yeah, I went in a circle but ended up with a different result because I equated sin^2 x - 1 to 1. Making so many mistakes tonight

rolpsy · Sep 10, 2012

Re: MX2 Integration Marathon

new question:

find

$\int^{1}_{0} \frac{x^{n-1}-1}{\ln(x)} \, \mathrm{d}x, \quad n>0$

or something easier

$\int \frac{2}{\left (\cos(x) - \sin(x) \right )^2} \, \mathrm{d}x$

asianese · Sep 10, 2012

Re: MX2 Integration Marathon

2 calls for an expansion of the denominator which results in 1-2sin2x by identities and double angles. Then a t=tanx substitution is made, which falls (pretty sure) into a perfect square on the bottom, leading to a linear power integral.

seanieg89 · Sep 16, 2012

Re: MX2 Integration Marathon

rolpsy said:
new question:

find

$\int^{1}_{0} \frac{x^{n-1}-1}{\ln(x)} \, \mathrm{d}x, \quad n>0$

Found a pretty slick way of doing this.

$Let $G(s):=\int_0^1\frac{x^{s-1}-1}{\log(x)}\,dx=\int_{-\infty}^0 \frac{e^{sx}-e^x}{x}\,dx$ for real $s\geq 1$. \\$G(1)$ is trivially $0$. Now for $s\geq 1$ we have:\\ $G'(s)=\int_{-\infty}^0\frac{\partial }{\partial s}\left(\frac{e^{sx}-e^x}{x}\right) \,dx=s^{-1}$ (by differentiating under the integral).\\So $G(s)=G(1)+\int_1^s t^{-1}\, dt=\log(s)$ for all $s\geq 1$.$

rolpsy · Sep 16, 2012

Re: MX2 Integration Marathon

good job

i did it a similar way:

$\begin{align*}\text{Set } G(t) = \int^{1}_{0} \frac{x^t-1}{\ln(x)}\, \mathrm{d}x \textup{, so that } G'(t) &= \frac{\mathrm{d} }{\mathrm{d} t}\int^{1}_{0} \frac{x^t-1}{\ln(x)} \, \mathrm{d}x\\&= \int^{1}_{0} \frac{\partial }{\partial t}\left (\frac{e^{t\ln(x)}-1}{\ln(x)} \right )\, \mathrm{d}x\\&= \int^{1}_{0} x^t \, \mathrm{d}x\\&=\frac{1}{t+1}\end{align*}$
etc.
It follows that I = G(n-1) = ln(n).

Also, asianese try and do the second one without t-results

Shadowdude · Sep 16, 2012

Re: MX2 Integration Marathon

what is this

leibniz rule?

seanieg89 · Sep 16, 2012

Re: MX2 Integration Marathon

There are many ways of justifying differentiating under the integral. Just use one that is general enough that it applies

. The one I use pretty much all the time is based on the dominated convergence theorem and suffices in most real-world applications.

barbernator · Sep 16, 2012

Re: MX2 Integration Marathon

the second one becomes a sec integration.

EDIT: no it doesnt

seanieg89 · Sep 16, 2012

Re: MX2 Integration Marathon

rolpsy said:
good job

i did it a similar way:

$\begin{align*}\text{Set } G(t) = \int^{1}_{0} \frac{x^t-1}{\ln(x)}\, \mathrm{d}x \textup{, so that } G'(t) &= \frac{\mathrm{d} }{\mathrm{d} t}\int^{1}_{0} \frac{x^t-1}{\ln(x)} \, \mathrm{d}x\\&= \int^{1}_{0} \frac{\partial }{\partial t}\left (\frac{e^{t\ln(x)}-1}{\ln(x)} \right )\, \mathrm{d}x\\&= \int^{1}_{0} x^t \, \mathrm{d}x\\&=\frac{1}{t+1}\end{align*}$
etc.
It follows that I = G(n-1) = ln(n).

Also, asianese try and do the second one without t-results

Yeah, the initial substitution of mine was unnecessary of course. Just something I like doing, prefer to work with exponential functions rather than logarithmic ones.

seanieg89 · Sep 16, 2012

Re: MX2 Integration Marathon

barbernator said:
the second one becomes a sec integration.

EDIT: no it doesnt

Easier.

nightweaver066 · Sep 16, 2012

Re: MX2 Integration Marathon

barbernator said:
the second one becomes a sec integration.

EDIT: no it doesnt

Talking about the second one rolpsy posted?

I think it becomes the standard sec^2 and sec2xtan2x

Cbb with paper lol

bleakarcher · Sep 16, 2012

Re: MX2 Integration Marathon

nightweaver066 said:
Talking about the second one rolpsy posted?

I think it becomes the standard sec^2 and sec2xtan2x

Cbb with paper lol

2/[cos^2(x)-2sin(x)cos(x)+sin^2(x)]=2sec^2(x)/[1-2tan(x)+tan^2(x)]=2sec^2(x)/[tan(x)-1]^2

Now it's easy.

D94 · Sep 16, 2012

Re: MX2 Integration Marathon

bleakarcher said:
2/[cos^2(x)-2sin(x)cos(x)+sin^2(x)]=2sec^2(x)/[1-2tan(x)+tan^2(x)]=2sec^2(x)/[tan(x)-1]^2

Now it's easy.

Alternatively, you could straightaway divide the top and bottom by cos²x.

bleakarcher · Sep 16, 2012

Re: MX2 Integration Marathon

D94 said:
Alternatively, you could straightaway divide the top and bottom by cos²x.

Yeah I guess that saves expanding [cos(x)-sin(x)]^2 haha.

HSC 2012-14 MX2 Integration Marathon (archive) (2 Viewers)

Administrator

Active Member

Member

Active Member

Well-Known Member

Account Closed

Member

Member

Σ

Well-Known Member

Member

Cult of Personality

Well-Known Member

Active Member

Well-Known Member

Well-Known Member

Well-Known Member

Active Member

New Member

Active Member

Users Who Are Viewing This Thread (Users: 0, Guests: 2)