-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2012-14 MX2 Integration Marathon (archive) (2 Viewers)
- Thread starter bleakarcher
- Start date
- Status
- Not open for further replies.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Let u= x^(n-2) du = (n-2)x^(n-3)
dv = x^2 (sqrt(1-x^3)) v= -(2/9) (1-x^3)^(3/2)
Un= (-(2/9)(1-x^3)^(3/2)x^(n-2))_1_0 +(2/9)(n-2) integral_1_0 ((1-x^3)^(3/2)(x^(n-3))
= 0 + 2/9 (n-2) (2/9)(n-2) (integral_1_0 ( (1-x^3)^(1/2))(1-x^3) x^(n-2)))
=(2/9)(n-2)[ integral _1_0 ((1-x^3)^(1/2) (x^(n-3)) - integral _1_0 (x^(n) ((1-x^3)^(1/2))]
=2/9 (n-2) (U_(n-3)-U_(n))
Rearranging (taking the U_n to the other side with its coefficient)
((2n+3)/9)U_(n)= (2/9)(n-2) (U_(n-3))
Simplifying U_n = ((2n-4)/(2n+3)) U_(n-3))
but n is not greater than or equal to 4. since U_(n-3) and n-3 > 0 but I dont know why it is greater than or equal to 5.
Sorry if you had to take a long time to read it (if you did read it).
Let u= x^(n-2) du = (n-2)x^(n-3)
dv = x^2 (sqrt(1-x^3)) v= -(2/9) (1-x^3)^(3/2)
Un= (-(2/9)(1-x^3)^(3/2)x^(n-2))_1_0 +(2/9)(n-2) integral_1_0 ((1-x^3)^(3/2)(x^(n-3))
= 0 + 2/9 (n-2) (2/9)(n-2) (integral_1_0 ( (1-x^3)^(1/2))(1-x^3) x^(n-2)))
=(2/9)(n-2)[ integral _1_0 ((1-x^3)^(1/2) (x^(n-3)) - integral _1_0 (x^(n) ((1-x^3)^(1/2))]
=2/9 (n-2) (U_(n-3)-U_(n))
Rearranging (taking the U_n to the other side with its coefficient)
((2n+3)/9)U_(n)= (2/9)(n-2) (U_(n-3))
Simplifying U_n = ((2n-4)/(2n+3)) U_(n-3))
but n is not greater than or equal to 4. since U_(n-3) and n-3 > 0 but I dont know why it is greater than or equal to 5.
Sorry if you had to take a long time to read it (if you did read it).
Re: MX2 Integration Marathon
As for the n greater than equal to 5, it is not as easy to integrate I_1 as compared to integrating I_2, thats probably why.
On the 8th line u made a tiny mistake, 1+2(n-2)/9=(2n+5)/9 instead of (2n+3)/9Let u= x^(n-2) du = (n-2)x^(n-3)
dv = x^2 (sqrt(1-x^3)) v= -(2/9) (1-x^3)^(3/2)
Un= (-(2/9)(1-x^3)^(3/2)x^(n-2))_1_0 +(2/9)(n-2) integral_1_0 ((1-x^3)^(3/2)(x^(n-3))
= 0 + 2/9 (n-2) (2/9)(n-2) (integral_1_0 ( (1-x^3)^(1/2))(1-x^3) x^(n-2)))
=(2/9)(n-2)[ integral _1_0 ((1-x^3)^(1/2) (x^(n-3)) - integral _1_0 (x^(n) ((1-x^3)^(1/2))]
=2/9 (n-2) (U_(n-3)-U_(n))
Rearranging (taking the U_n to the other side with its coefficient)
((2n+3)/9)U_(n)= (2/9)(n-2) (U_(n-3))
Simplifying U_n = ((2n-4)/(2n+3)) U_(n-3))
but n is not greater than or equal to 4. since U_(n-3) and n-3 > 0 but I dont know why it is greater than or equal to 5.
Sorry if you had to take a long time to read it (if you did read it).
As for the n greater than equal to 5, it is not as easy to integrate I_1 as compared to integrating I_2, thats probably why.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Sorry for the mistake. Oh ok I though that but I though it should work so I discarded that thought.On the 8th line u made a tiny mistake, 1+2(n-2)/9=(2n+5)/9 instead of (2n+3)/9
As for the n greater than equal to 5, it is not as easy to integrate I_1 as compared to integrating I_2, thats probably why.
Re: MX2 Integration Marathon
Yeh the formula should work even for n>=3 but to end up with and integral we can easily evaluate, we would want to sub a number in the form n=3k+2Sorry for the mistake. Oh ok I though that but I though it should work so I discarded that thought.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Let u^2= 1+4x (u.du)/2 = dx when x=6, u= 5 when x= 2 u= 3
Integral _5_3((ln(-1+u) -ln2) u.du/2)
--------------------------------------------------------------
Let integral _5 _3 (u.ln(u-1))= I
For I,
Let y= ln (u-1) dy=1/(u-1)
Let dz= u z= (u^2)/2
therefore I= [((u^2)/2)ln(u-1)]_5_3 - integral ((u^2)/2(u-1))_5 _3
= (41/2)ln(2) - integral (u + u/(u-1))_5_3
= 20ln(2) -5
-----------------------------------------------
M= (1/2) (20ln(2)-5) - 4ln(2) = 6 ln(2) - 5/2
____________________________________________________________________
Sorry for the messy work. Possibly and probably some mistakes due to bracketing problems that I faced.
LET M BE the INTEGRAL PROVIDED.
Let u^2= 1+4x (u.du)/2 = dx when x=6, u= 5 when x= 2 u= 3
Integral _5_3((ln(-1+u) -ln2) u.du/2)
--------------------------------------------------------------
Let integral _5 _3 (u.ln(u-1))= I
For I,
Let y= ln (u-1) dy=1/(u-1)
Let dz= u z= (u^2)/2
therefore I= [((u^2)/2)ln(u-1)]_5_3 - integral ((u^2)/2(u-1))_5 _3
= (41/2)ln(2) - integral (u + u/(u-1))_5_3
= 20ln(2) -5
-----------------------------------------------
M= (1/2) (20ln(2)-5) - 4ln(2) = 6 ln(2) - 5/2
____________________________________________________________________
Sorry for the messy work. Possibly and probably some mistakes due to bracketing problems that I faced.
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
I think you have made a mistakeLET M BE the INTEGRAL PROVIDED.
Let u^2= 1+4x (u.du)/2 = dx when x=6, u= 5 when x= 2 u= 3
Integral _5_3((ln(-1+u) -ln2) u.du/2)
--------------------------------------------------------------
Let integral _5 _3 (u.ln(u-1))= I
For I,
Let y= ln (u-1) dy=1/(u-1)
Let dz= u z= (u^2)/2
therefore I= [((u^2)/2)ln(u-1)]_5_3 - integral ((u^2)/2(u-1))_5 _3
= (41/2)ln(2) - integral (u - u/(u-1))_5_3
= (41/2)ln(2) - 6 + ln (3/5)
-----------------------------------------------
M= (41/2)ln(2) -6 + ln (3/5) -16 ln (2) = (9/2)ln(2) + ln(3/5) -6
____________________________________________________________________
Sorry for the messy work. Possibly and probably some mistakes due to bracketing problems that I faced.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Used curve sketching to draw the graph found an approximate area to find integral. Answer way off and got a negative answer that doesnt correspond to the answer I got.LET M BE the INTEGRAL PROVIDED.
Let u^2= 1+4x (u.du)/2 = dx when x=6, u= 5 when x= 2 u= 3
Integral _5_3((ln(-1+u) -ln2) u.du/2)
--------------------------------------------------------------
Let integral _5 _3 (u.ln(u-1))= I
For I,
Let y= ln (u-1) dy=1/(u-1)
Let dz= u z= (u^2)/2
therefore I= [((u^2)/2)ln(u-1)]_5_3 - integral ((u^2)/2(u-1))_5 _3
= (41/2)ln(2) - integral (u - u/(u-1))_5_3
= (41/2)ln(2) - 6 + ln (3/5)
-----------------------------------------------
M= (41/2)ln(2) -6 + ln (3/5) -16 ln (2) = (9/2)ln(2) + ln(3/5) -6
____________________________________________________________________
Sorry for the messy work. Possibly and probably some mistakes due to bracketing problems that I faced.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Think i fixed it.I think you have made a mistake
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: MX2 Integration Marathon
The method I had in mind was recognising that the argument inside the logarithm looks like a solution to a quadratic equation, namely

So it makes sense then to just make the substitution

 \ du )

Then simple by parts from there
Yep that is correct.Think i fixed it.
The method I had in mind was recognising that the argument inside the logarithm looks like a solution to a quadratic equation, namely
So it makes sense then to just make the substitution
Then simple by parts from there
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Oh ok. I didnt see that. I have never seen anyone use that. That a really great method. Cant rep. I would If i could.Yep that is correct.
The method I had in mind was recognising that the argument inside the logarithm looks like a solution to a quadratic equation, namely
So it makes sense then to just make the substitution
Then simple by parts from there
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Yep thanks.6ln2-5/2? Just use u=ln(...) And hence x=e^u+e^2u then IBP
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: MX2 Integration Marathon
.In this question we compute the Dirichlet integral using high school methods.
Note: n ranges over the non-negative integers.
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
= sin(2n-1)x cos(2x) - cos(2n-1)xsin(2x)
= sin (2n-1)x (1-2sin^(2) x) - cos (2n-1)x(2cosxsinx)
Expanding we get:
sin (2n-1)x - 2sin(2n-1)xsin^(2)x + 2cos(2n-1)xsinxcosx
Now sin(2n+1)x/sinx = sin (2n-1)x / sin(x) - 2sin (2n-1)xsinx + 2cos(2n-1)xcosx
But this consists of cos(a+b)
Therefore = sin (2n-1)x/sin (x) -2 cos(2nx)
Integral _pi/2_0 sin (2(n-1)+1)x/sin(x) -2cos(2nx) dx
= U_(n-1) + 2 [ sin(2nx)/2n] _ pi/2_0
= U_(n-1)
huh? now? Looks like I did something wrong. how can integral of u_n be equal to u_(n-1) hm? and how do I continue .
isnt 2n-1 always odd in my answer therefore i get 1 as answer/
And also any other quicker ways. This way took me a long time to think of because first time I did it I expanded straight away. Then thought about the ways I could integrate and saw that the only way I could do this and get rid of the sinx at bottom was by using double angle formula so yeh I had to go through a long process. Any other shorter methods?
1) sin (2n+1)x = sin (2n-1 +2)x
= sin(2n-1)x cos(2x) - cos(2n-1)xsin(2x)
= sin (2n-1)x (1-2sin^(2) x) - cos (2n-1)x(2cosxsinx)
Expanding we get:
sin (2n-1)x - 2sin(2n-1)xsin^(2)x + 2cos(2n-1)xsinxcosx
Now sin(2n+1)x/sinx = sin (2n-1)x / sin(x) - 2sin (2n-1)xsinx + 2cos(2n-1)xcosx
But this consists of cos(a+b)
Therefore = sin (2n-1)x/sin (x) -2 cos(2nx)
Integral _pi/2_0 sin (2(n-1)+1)x/sin(x) -2cos(2nx) dx
= U_(n-1) + 2 [ sin(2nx)/2n] _ pi/2_0
= U_(n-1)
huh? now? Looks like I did something wrong. how can integral of u_n be equal to u_(n-1) hm? and how do I continue .
isnt 2n-1 always odd in my answer therefore i get 1 as answer/
And also any other quicker ways. This way took me a long time to think of because first time I did it I expanded straight away. Then thought about the ways I could integrate and saw that the only way I could do this and get rid of the sinx at bottom was by using double angle formula so yeh I had to go through a long process. Any other shorter methods?
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: MX2 Integration Marathon

}{\sin(x)} ~dx)

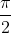
1) sin (2n+1)x = sin (2n-1 +2)x
= sin(2n-1)x cos(2x) - cos(2n-1)xsin(2x)
= sin (2n-1)x (1-2sin^(2) x) - cos (2n-1)x(2cosxsinx)
Expanding we get:
sin (2n-1)x - 2sin(2n-1)xsin^(2)x + 2cos(2n-1)xsinxcosx
Now sin(2n+1)x/sinx = sin (2n-1)x / sin(x) - 2sin (2n-1)xsinx + 2cos(2n-1)xcosx
But this consists of cos(a+b)
Therefore = sin (2n-1)x/sin (x) -2 cos(2nx)
Integral _pi/2_0 sin (2(n-1)+1)x/sin(x) -2cos(2nx) dx
= U_(n-1) + 2 [ sin(2nx)/2n] _ pi/2_0
= U_(n-1)
huh? now? Looks like I did something wrong. how can integral of u_n be equal to u_(n-1) hm? and how do I continue .
isnt 2n-1 always odd in my answer therefore i get 1 as answer/
hit patel
New Member
- Joined
- Mar 14, 2012
- Messages
- 568
- Gender
- Male
- HSC
- 2014
- Uni Grad
- 2018
Re: MX2 Integration Marathon
Hahahah what so I actually had the answer the whole time and I went through all that. Hahaha I used that fact you just showed in the answer I wrote. Look at the bottom of my answer. What was I thinking? But shouldnt I still get the same answer?
juantheron
Active Member
- Joined
- Feb 9, 2012
- Messages
- 259
- Gender
- Male
- HSC
- N/A
Re: MX2 Integration Marathon
\sqrt{\cos%202%20\phi}}\right)d\phi%20=%200$)
- Status
- Not open for further replies.

