Re: 2012 HSC MX2 Marathon
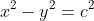
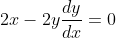
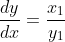
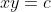
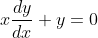
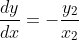

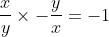

Woo new question XDWhat happened to this thread?

Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Woo new question XDWhat happened to this thread?

I've seen this question before... I don't quite remember when.If 0, z_1, z_2 and z_3 lie on a circle then prove that the points 1/z_1, 1/z_2 and 1/z_3 are collinear. (z_1, z_2, z_3 are non zero complex numbers)
I couldn't think of any to postPerhaps you can post up a question now.
question is in patel and terry leeI've seen this question before... I don't quite remember when.
Also, no "Hence find the exact value of":Easy questions
(a).If w is a complex root of z^5 -1=0 with the smallest positive argument, show that w^2 ,w^3 and 2^4 are the other complex roots.And hence prove that 1+w^2+w^3+w^4=0
(b).Find the quadratic equation whose roots are a=w+w^4 and B=w^2+w^3
<a href="http://www.codecogs.com/eqnedit.php?latex=\\ z^5=1=cis0=cis2k\pi\\ z=(cis2k\pi)^{\frac{1}{5}}=cis\frac{2}{5}k\pi_{(k=0,1,2,3,4,)}~\textrm{(By De Moivre's theorem)}\\ ~\\ z_1=cis0=1~~~~~~ z_2=cis\frac{2}{5}\pi~~~~~ z_3=cis\frac{4}{5}\pi~~~~~ z_4=cis\frac{6}{5}\pi~~~~~ z_5=cis\frac{8}{5}\pi\\ ~\\ \therefore w=z_2=cis\frac{2}{5}\pi~\textrm{(Since it's the root with the smallest positive argument)}\\ z_3=(z_2)^2,~~~~~ z_4=(z_2)^3,~~~~~ z_5=(z_2)^4~\textrm{(By De Doivre's theorem)}\\ \therefore \textrm{the other complex roots are}~w^2,w^3, w^4 ~\\~\\~\\~\\ \frac{-b}{a}=\alpha@plus;\beta=w@plus;w^2@plus;w^3@plus;w^4=-1~(\textrm{since}~1@plus;w@plus;w^2@plus;w^3@plus;w^4=0)\\ \therefore b=1\\ ~\\ \frac{c}{a}=\alpha \beta=(w@plus;w^4)(w^2@plus;w^3)\\ =w^3@plus;w^4@plus;w^6@plus;w^7=w^3@plus;w^4@plus;w@plus;w^2=-1~(\textrm{since}~w^5=1)\\ \therefore c=-1\\~\\ \therefore \textrm{the required quadratic equation is}~x^2@plus;x-1" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ z^5=1=cis0=cis2k\pi\\ z=(cis2k\pi)^{\frac{1}{5}}=cis\frac{2}{5}k\pi_{(k=0,1,2,3,4,)}~\textrm{(By De Moivre's theorem)}\\ ~\\ z_1=cis0=1~~~~~~ z_2=cis\frac{2}{5}\pi~~~~~ z_3=cis\frac{4}{5}\pi~~~~~ z_4=cis\frac{6}{5}\pi~~~~~ z_5=cis\frac{8}{5}\pi\\ ~\\ \therefore w=z_2=cis\frac{2}{5}\pi~\textrm{(Since it's the root with the smallest positive argument)}\\ z_3=(z_2)^2,~~~~~ z_4=(z_2)^3,~~~~~ z_5=(z_2)^4~\textrm{(By De Doivre's theorem)}\\ \therefore \textrm{the other complex roots are}~w^2,w^3, w^4 ~\\~\\~\\~\\ \frac{-b}{a}=\alpha+\beta=w+w^2+w^3+w^4=-1~(\textrm{since}~1+w+w^2+w^3+w^4=0)\\ \therefore b=1\\ ~\\ \frac{c}{a}=\alpha \beta=(w+w^4)(w^2+w^3)\\ =w^3+w^4+w^6+w^7=w^3+w^4+w+w^2=-1~(\textrm{since}~w^5=1)\\ \therefore c=-1\\~\\ \therefore \textrm{the required quadratic equation is}~x^2+x-1" title="\\ z^5=1=cis0=cis2k\pi\\ z=(cis2k\pi)^{\frac{1}{5}}=cis\frac{2}{5}k\pi_{(k=0,1,2,3,4,)}~\textrm{(By De Moivre's theorem)}\\ ~\\ z_1=cis0=1~~~~~~ z_2=cis\frac{2}{5}\pi~~~~~ z_3=cis\frac{4}{5}\pi~~~~~ z_4=cis\frac{6}{5}\pi~~~~~ z_5=cis\frac{8}{5}\pi\\ ~\\ \therefore w=z_2=cis\frac{2}{5}\pi~\textrm{(Since it's the root with the smallest positive argument)}\\ z_3=(z_2)^2,~~~~~ z_4=(z_2)^3,~~~~~ z_5=(z_2)^4~\textrm{(By De Doivre's theorem)}\\ \therefore \textrm{the other complex roots are}~w^2,w^3, w^4 ~\\~\\~\\~\\ \frac{-b}{a}=\alpha+\beta=w+w^2+w^3+w^4=-1~(\textrm{since}~1+w+w^2+w^3+w^4=0)\\ \therefore b=1\\ ~\\ \frac{c}{a}=\alpha \beta=(w+w^4)(w^2+w^3)\\ =w^3+w^4+w^6+w^7=w^3+w^4+w+w^2=-1~(\textrm{since}~w^5=1)\\ \therefore c=-1\\~\\ \therefore \textrm{the required quadratic equation is}~x^2+x-1" /></a>Easy questions
(a).If w is a complex root of z^5 -1=0 with the smallest positive argument, show that w^2 ,w^3 and 2^4 are the other complex roots.And hence prove that 1+w^2+w^3+w^4=0
(b).Find the quadratic equation whose roots are a=w+w^4 and B=w^2+w^3
that first one from cambridge polynomials?:/
And for something a little harder...
Interested in seeing different ways people solve it.
Yes it is hahaha. Got asked to do it last night and thought it was quite nice.that first one from cambridge polynomials?:/
well done but you didnt prove that w+w^2+w^3+w^4=-1<a href="http://www.codecogs.com/eqnedit.php?latex=\\ z^5=1=cis0=cis2k\pi\\ z=(cis2k\pi)^{\frac{1}{5}}=cis\frac{2}{5}k\pi_{(k=0,1,2,3,4,)}~\textrm{(By De Moivre's theorem)}\\ ~\\ z_1=cis0=1~~~~~~ z_2=cis\frac{2}{5}\pi~~~~~ z_3=cis\frac{4}{5}\pi~~~~~ z_4=cis\frac{6}{5}\pi~~~~~ z_5=cis\frac{8}{5}\pi\\ ~\\ \therefore w=z_2=cis\frac{2}{5}\pi~\textrm{(Since it's the root with the smallest positive argument)}\\ z_3=(z_2)^2,~~~~~ z_4=(z_2)^3,~~~~~ z_5=(z_2)^4~\textrm{(By De Doivre's theorem)}\\ \therefore \textrm{the other complex roots are}~w^2,w^3, w^4 ~\\~\\~\\~\\ \frac{-b}{a}=\alpha@plus;\beta=w@plus;w^2@plus;w^3@plus;w^4=-1~(\textrm{since}~1@plus;w@plus;w^2@plus;w^3@plus;w^4=0)\\ \therefore b=1\\ ~\\ \frac{c}{a}=\alpha \beta=(w@plus;w^4)(w^2@plus;w^3)\\ =w^3@plus;w^4@plus;w^6@plus;w^7=w^3@plus;w^4@plus;w@plus;w^2=-1~(\textrm{since}~w^5=1)\\ \therefore c=-1\\~\\ \therefore \textrm{the required quadratic equation is}~x^2@plus;x-1" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\\ z^5=1=cis0=cis2k\pi\\ z=(cis2k\pi)^{\frac{1}{5}}=cis\frac{2}{5}k\pi_{(k=0,1,2,3,4,)}~\textrm{(By De Moivre's theorem)}\\ ~\\ z_1=cis0=1~~~~~~ z_2=cis\frac{2}{5}\pi~~~~~ z_3=cis\frac{4}{5}\pi~~~~~ z_4=cis\frac{6}{5}\pi~~~~~ z_5=cis\frac{8}{5}\pi\\ ~\\ \therefore w=z_2=cis\frac{2}{5}\pi~\textrm{(Since it's the root with the smallest positive argument)}\\ z_3=(z_2)^2,~~~~~ z_4=(z_2)^3,~~~~~ z_5=(z_2)^4~\textrm{(By De Doivre's theorem)}\\ \therefore \textrm{the other complex roots are}~w^2,w^3, w^4 ~\\~\\~\\~\\ \frac{-b}{a}=\alpha+\beta=w+w^2+w^3+w^4=-1~(\textrm{since}~1+w+w^2+w^3+w^4=0)\\ \therefore b=1\\ ~\\ \frac{c}{a}=\alpha \beta=(w+w^4)(w^2+w^3)\\ =w^3+w^4+w^6+w^7=w^3+w^4+w+w^2=-1~(\textrm{since}~w^5=1)\\ \therefore c=-1\\~\\ \therefore \textrm{the required quadratic equation is}~x^2+x-1" title="\\ z^5=1=cis0=cis2k\pi\\ z=(cis2k\pi)^{\frac{1}{5}}=cis\frac{2}{5}k\pi_{(k=0,1,2,3,4,)}~\textrm{(By De Moivre's theorem)}\\ ~\\ z_1=cis0=1~~~~~~ z_2=cis\frac{2}{5}\pi~~~~~ z_3=cis\frac{4}{5}\pi~~~~~ z_4=cis\frac{6}{5}\pi~~~~~ z_5=cis\frac{8}{5}\pi\\ ~\\ \therefore w=z_2=cis\frac{2}{5}\pi~\textrm{(Since it's the root with the smallest positive argument)}\\ z_3=(z_2)^2,~~~~~ z_4=(z_2)^3,~~~~~ z_5=(z_2)^4~\textrm{(By De Doivre's theorem)}\\ \therefore \textrm{the other complex roots are}~w^2,w^3, w^4 ~\\~\\~\\~\\ \frac{-b}{a}=\alpha+\beta=w+w^2+w^3+w^4=-1~(\textrm{since}~1+w+w^2+w^3+w^4=0)\\ \therefore b=1\\ ~\\ \frac{c}{a}=\alpha \beta=(w+w^4)(w^2+w^3)\\ =w^3+w^4+w^6+w^7=w^3+w^4+w+w^2=-1~(\textrm{since}~w^5=1)\\ \therefore c=-1\\~\\ \therefore \textrm{the required quadratic equation is}~x^2+x-1" /></a>
You forgot the +C.^This? I am leaving the forum if I don't get this answer correct. I've been puzzled by this for a while now. I hope I am not over thinking.
asdogfajogjagrddgsYou forgot the +C.
Now get out of the forums.
http://community.boredofstudies.org/showthread.php?t=234259how do you guys "write mathematical notation and symbols on here. I'm currently stuck to using z^2
Thanks brah
