-
Interested in being a marker for this year's BoS Maths Trials? Let us know before 31 August, see this thread for details
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013-14 MX1 Marathon (archive) (1 Viewer)
- Thread starter SpiralFlex
- Start date
- Status
- Not open for further replies.
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 3U Marathon Thread
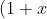^k + (1+x)^{k+1} + (1+x)^{k+2} + ... + (1+x)^n = \frac{(1+x)^k[(1+x)^{n-k+1}-1]}{x}) by sum of a GP.
by sum of a GP.
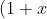^k + (1+x)^{k+1} + (1+x)^{k+2} + ... + (1+x)^n = \frac{(1+x)^{n+1}}{x} - \frac{(1+x)^k}{x})
Equating the co-efficients of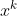 :
:

Note that in^{n+1}}{x}) the co-efficient of
the co-efficient of 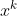 is
is  since you have to divide by
since you have to divide by  which means you must take the
which means you must take the  term of the numerator.
term of the numerator.
Also in^k}{x}) there is no co-efficient of
there is no co-efficient of 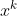 as the highest power of the numerator is
as the highest power of the numerator is  but you divide by
but you divide by  , making the highest power of the whole expression only
, making the highest power of the whole expression only  .
.
EDIT: Have I already posted this question? I have a feeling I already have.
Equating the co-efficients of
Note that in
Also in
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 3U Marathon Thread
Essentially if you continue, you end up removing this amount:
^2 + 2^2(\frac{1}{3})^3 + 2^3(\frac{1}{3})^4 +...)
Which can be expressed as such:
^{k+1})
Re-arranging:


^k)


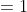
Although you could arrive at this intuitively, a proper mathematical proof is probably better.
I kinda rushed this, so hope I haven't made a mistake:
Essentially if you continue, you end up removing this amount:
Which can be expressed as such:
Re-arranging:
Although you could arrive at this intuitively, a proper mathematical proof is probably better.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 3U Marathon Thread
At each step, your figure is a finite union of intervals. By removing the middle third of each we are multiplying the sum of the lengths of the remaining intervals by 2/3. Hence after n iterations, the total "length" we have removed from our figure is 1-(2/3)^n. This trivially tends to 1 as n->inf.
Alternatively:I kinda rushed this, so hope I haven't made a mistake:
Essentially if you continue, you end up removing this amount:
Which can be expressed as such:
Re-arranging:
Although you could arrive at this intuitively, a proper mathematical proof is probably better.
At each step, your figure is a finite union of intervals. By removing the middle third of each we are multiplying the sum of the lengths of the remaining intervals by 2/3. Hence after n iterations, the total "length" we have removed from our figure is 1-(2/3)^n. This trivially tends to 1 as n->inf.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 3U Marathon Thread
Consider picking k+1 numbers out of the numbers {1,2,...,n+1}.
The right hand side of your equation is clearly equal to the number of ways of doing this.
Now for any given choice of k+1 numbers, the highest number chosen must be some j with k+1 =< j =< n+1. In each of these cases, we must select the remaining k numbers to be chosen from the j-1 numbers smaller than j.
Summing up the number of ways of doing this for j=k+1,...,n+1 yields the LHS of your equation.
Here's a combinatorial proof for variety.
EDIT: Have I already posted this question? I have a feeling I already have.
Consider picking k+1 numbers out of the numbers {1,2,...,n+1}.
The right hand side of your equation is clearly equal to the number of ways of doing this.
Now for any given choice of k+1 numbers, the highest number chosen must be some j with k+1 =< j =< n+1. In each of these cases, we must select the remaining k numbers to be chosen from the j-1 numbers smaller than j.
Summing up the number of ways of doing this for j=k+1,...,n+1 yields the LHS of your equation.
Capt Rifle
Member
- Joined
- Jul 17, 2012
- Messages
- 398
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
that is a good question...not sure where to start lol
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Yeah as you can see, it isn't necessarily hard, just a nice little result.I kinda rushed this, so hope I haven't made a mistake:
Essentially if you continue, you end up removing this amount:
Which can be expressed as such:
Re-arranging:
Although you could arrive at this intuitively, a proper mathematical proof is probably better.
Very nice. (the only reason why I ask for a possible combinatorial proof is because I want someone to show me one)Here's a combinatorial proof for variety.
Consider picking k+1 numbers out of the numbers {1,2,...,n+1}.
The right hand side of your equation is clearly equal to the number of ways of doing this.
Now for any given choice of k+1 numbers, the highest number chosen must be some j with k+1 =< j =< n+1. In each of these cases, we must select the remaining k numbers to be chosen from the j-1 numbers smaller than j.
Summing up the number of ways of doing this for j=k+1,...,n+1 yields the LHS of your equation.
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 874
- Gender
- Male
- HSC
- 2010
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 874
- Gender
- Male
- HSC
- 2010
Re: HSC 2013 3U Marathon Thread
Let M bet the midpoint of a chord PQ in a circle
Two chords AD and BC are drawn so that they intersect at M
AB and CD intersect the chord PQ at X and Y respectively
Show that M is the midpoint of XY
Let M bet the midpoint of a chord PQ in a circle
Two chords AD and BC are drawn so that they intersect at M
AB and CD intersect the chord PQ at X and Y respectively
Show that M is the midpoint of XY
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 3U Marathon Thread
As you have currently phrased the question, X and Y are both the point M itself...Let M be the midpoint of chord PQ in a circle
AB and CD are two other chords which pass through M
AB and CD intersect the chord PQ at points X and Y respectively
Show that M is the midpoint of XY
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 874
- Gender
- Male
- HSC
- 2010
Re: HSC 2013 3U Marathon Thread
hopefully it makes some sense now
thanks for that , don't know what I was thinkingAs you have currently phrased the question, X and Y are both the point M itself...
hopefully it makes some sense now
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 3U Marathon Thread
It doesn't, as AB and CD are arbitrary the claim is false.thanks for that , don't know what I was thinking
hopefully it makes some sense now
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 874
- Gender
- Male
- HSC
- 2010
Re: HSC 2013 3U Marathon Thread
Let M bet the midpoint of a chord PQ in a circle
Two chords AD and BC are drawn so that they intersect at M
AB and CD intersect the chord PQ at X and Y respectively
Show that M is the midpoint of XY
Could you check this?It doesn't, as AB and CD are arbitrary the claim is false.
Let M bet the midpoint of a chord PQ in a circle
Two chords AD and BC are drawn so that they intersect at M
AB and CD intersect the chord PQ at X and Y respectively
Show that M is the midpoint of XY
Last edited:
funnytomato
Active Member
- Joined
- Jan 21, 2011
- Messages
- 874
- Gender
- Male
- HSC
- 2010
Re: HSC 2013 3U Marathon Thread


Capt Rifle
Member
- Joined
- Jul 17, 2012
- Messages
- 398
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 3U Marathon Thread
Use mathematical induction and the product rule for differentiation to prove that
<a href="http://www.codecogs.com/eqnedit.php?latex=\frac{d}{dx}(x^n)=nx^{n-1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\frac{d}{dx}(x^n)=nx^{n-1}" title="\frac{d}{dx}(x^n)=nx^{n-1}" /></a>
For all positive integers n.
I believe this is more 3u than 4u, anyone else agree?
Use mathematical induction and the product rule for differentiation to prove that
<a href="http://www.codecogs.com/eqnedit.php?latex=\frac{d}{dx}(x^n)=nx^{n-1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\frac{d}{dx}(x^n)=nx^{n-1}" title="\frac{d}{dx}(x^n)=nx^{n-1}" /></a>
For all positive integers n.
I believe this is more 3u than 4u, anyone else agree?
Nws m8
Banned
- Joined
- Oct 21, 2012
- Messages
- 494
- Gender
- Male
- HSC
- 2012
- Uni Grad
- 2018
Re: HSC 2013 3U Marathon Thread
this IS 3u, I remember doing this in 3u, too easy for 4u m8Use mathematical induction and the product rule for differentiation to prove that
<a href="http://www.codecogs.com/eqnedit.php?latex=\frac{d}{dx}(x^n)=nx^{n-1}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\frac{d}{dx}(x^n)=nx^{n-1}" title="\frac{d}{dx}(x^n)=nx^{n-1}" /></a>
For all positive integers n.
I believe this is more 3u than 4u, anyone else agree?
- Status
- Not open for further replies.
