RealiseNothing
what is that?It is Cowpea
Re: HSC 2014 4U Marathon
 are positive reals such that
are positive reals such that 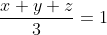
Prove that:
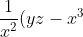 + \frac{1}{y^2}(xz-y^3) + \frac{1}{z^2}(xy-z^3) \geq 0)
Prove that:
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
are positive reals such that
Prove that:
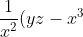 + \frac{1}{y^2}(xz-y^3) + \frac{1}{z^2}(xy-z^3) \geq 0)
Yep that was a bit on the easier side I guess. It's hard trying to think of a really challenging inequality, I'm trying though lol.
Prove that:Hate to spoil the party, but you guys reckon you could be a bit more inclusive of the 2014ers? At the moment, it's mainly post-HSC people that are driving this thread.
Some IMO from the 60's and 70's etc are quite doable.Some national olympiad problems from Copy of Kalva homepage are the perfect level for this thread. Check that any given problem can be done using only mx2 stuff though. And probably avoid IMO stuff outside of Q1,4.
Oh definitely. There is a huge shift in difficulty somewhere between 75 and 95. (I probably still can't do most modern Q6s, and certainly not in the exam conditions.) I meant any inequality that is not Q1 or 4 in relatively recent olympiads.Some IMO from the 60's and 70's etc are quite doable.
Entirely?Hate to spoil the party, but you guys reckon you could be a bit more inclusive of the 2014ers? At the moment, it's mainly post-HSC people that are driving this thread.
Ah right. Also do you know why there was a massive shift around then?Oh definitely. There is a huge shift in difficulty somewhere between 75 and 95. (I probably still can't do most modern Q6s, and certainly not in the exam conditions.) I meant any inequality that is not Q1 or 4 in relatively recent olympiads.
Beats me. Maybe the fact that countries were starting to prepare more intensively meant the organising committee thought it needed to be made harder. There is probably an explanation online somewhere but am too lazy to look.Ah right. Also do you know why there was a massive shift around then?
I think we should post 2014'er only questions and questions in general for anyone. The above is my 2014'er question. Here is a question from seanie's link for everyone:Prove that:
2014'ers only.
Bonus points: Use circle geometry.
Problem is when I do try and engage the 2014er friendly topics no one answers my questions, nor are they trying to post questions themselves.Hate to spoil the party, but you guys reckon you could be a bit more inclusive of the 2014ers? At the moment, it's mainly post-HSC people that are driving this thread.
I think I got itI think we should post 2014'er only questions and questions in general for anyone. The above is my 2014'er question. Here is a question from seanie's link for everyone:
Prove for any positive realsthat:
^2}{2x^2 + (y+z)^2} + \frac{(2y+x+z)^2}{2y^2+(x+z)^2} + \frac{(2z+x+y)^2}{2z^2+(x+y)^2} \leq 8)
One way I've found to do this is to consider the differentiation by first principles ofHow do I evaluate this without l'hopital's? View attachment 29606
haha substitutions can be quite powerfulgg
that is all

