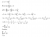Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon
y= -(2A/C) x
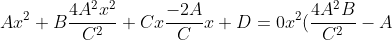 = -D )
and thus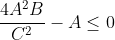
The idea is spot on, my algebra was thoughNot sure about my inequality result, but I think my solution is wrongView attachment 29810
y= -(2A/C) x
and thus
Last edited: