Ok, I decided to undergo a proof by induction:

If it is quadrilateral, it is obvious that there is only at most 1 point the diagonals can all intersect, and:

Hence it is true for n=4
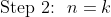
We assume true that a k sided convex polygon can have at most
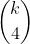
diagonal intersections.
k sided polygon diagram
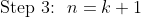
Ok, so we need to construct a k+1 sided polygon from the k sided polygon. We can do this by 'breaking one side into 2 pieces and joining it on' as shown:
k+1 sided polygon diagram
So we have done so as shown above. Now keep in mind that we already have kC4 intersections from before (I didn't show it).
So lets construct the k-2 number of diagonals from the new point we have constructed.
Ok, now notice the first red line I have constructed. Indeed there are: k-2 intersections from diagonals FROM THE OTHER POINTS
Look at the next red line, it is you could say 'defending' 2 points behind the second red line, there are (k-3) + (k-3) intersections from other points (k-3) for each point.
The pattern continues, the new intersections created by the new point is:
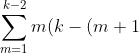) )
So lets evaluate this:

I can evaluate sum of squares through telescoping sum but I will skip this (or I could just rote the formula and put it down)
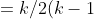(k-2) -1/2(k-1)(k-2) - \sum_{m=1}^{k-2}m^2 )
I plug in the formula, simplify and I end up with:
^2(k-2) - 1/6 (k-2)(k-1)(2k-3) )
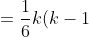(k-2) )
(srs)

And remember we already have
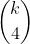
intersections from before.
So NOW we have:
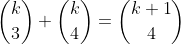
(by Pascal or otherwise)

=======
So satisfying to finally get the answer out of all that
 Prove Fermat's Last Theorem$ \ \ \ \ \fbox{442} )

