Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
RealiseNothing
what is that?It is Cowpea
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Last question - last part yeah, I thought the intuition you needed would be great for a marathon question (short and sweet).CSSA 2012 iirc?
Re: HSC 2013 4U Marathon
Here's a further hint:
 = \lim_{x \to a} \frac{f(x)-f(a)}{x-a} \\ \\ \text{ We can rethink this as } \lim_{x\to a}\frac{f(x)-f(a) - f'(a)(x-a)}{x-a}=0 \\ \\\text{ Note that f(a) and f'(a) are constant so f(a) + f'(a)(x-a) is a polynomial in x-a}$$)
EDIT: So I read the second step and the idea of adding and subtracting the same term was good and is a pretty standard technique in analysis. However, it still has some subtle errors. Firstly, while this is mostly a superficial error, in your assumption your said f is only k times differentiable, this condition is too strong and infact contradicts what your trying to prove. The assumption should be f is k times differentiable. Secondly, there is a more subtle error and I leave it as an exercise to find it. but note that as it stands, if your n=k+1 step was correct then this would imply that any function that is differentiable once would be differentiable to all orders. (While this is obviously wrong to me, I'm unsure if a HSC student would have run across a counter example since this tends to be true for most functions encountered at a hsc level.)
I didn't read the rest but i can already tell your confused. Unsurprising since this question is definitely out of the scope of the hsc. (note that you said f'(a)=0, which is note true in general).This is my attempt:
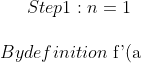=\lim_{x\to a} \frac{f(x)-f(a)}{x-a} \\ $There must exist a polynomial P, of degree 1, in the form$ \ \ P(x-a) \ \ $such that$ \\ P(x-a)=f(a) \ \ \ $IFF$ \ \ \ x \to a )
-P(x-a)}{|x-a|} = f'(a) \\ \\ \text{Now, if f(x) is only differentiable once at x=a, then f'(a)=0 as shown above. Hence statement is true for n=1} )
Here's a further hint:
EDIT: So I read the second step and the idea of adding and subtracting the same term was good and is a pretty standard technique in analysis. However, it still has some subtle errors. Firstly, while this is mostly a superficial error, in your assumption your said f is only k times differentiable, this condition is too strong and infact contradicts what your trying to prove. The assumption should be f is k times differentiable. Secondly, there is a more subtle error and I leave it as an exercise to find it. but note that as it stands, if your n=k+1 step was correct then this would imply that any function that is differentiable once would be differentiable to all orders. (While this is obviously wrong to me, I'm unsure if a HSC student would have run across a counter example since this tends to be true for most functions encountered at a hsc level.)
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
EDIT: And I am guessing that:
=\sum_{k=0}^{n} f^{(k)}(a) x^k )
??
Ah I see there, well you just posted the solution for Step 1, if I get rid of the strength of the assumption and loosen it up is it correct?I didn't read the rest but i can already tell your confused. Unsurprising since this question is definitely out of the scope of the hsc. (note that you said f'(a)=0, which is note true in general).
Here's a further hint:
EDIT: So I read the second step and the idea of adding and subtracting the same term was good and is a pretty standard technique in analysis. However, it still has some subtle errors. Firstly, while this is mostly a superficial error, in your assumption your said f is only k times differentiable, this condition is too strong and infact contradicts what your trying to prove. The assumption should be f is k times differentiable. Secondly, there is a more subtle error and I leave it as an exercise to find it. but note that as it stands, if your n=k+1 step was correct then this would imply that any function that is differentiable once would be differentiable to all orders. (While this is obviously wrong to me, I'm unsure if a HSC student would have run across a counter example since this tends to be true for most functions encountered at a hsc level.)
EDIT: And I am guessing that:
??
Last edited:
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
Missing a factor of k!. Perhaps I should have given the form of the polynomial in my question but anyway, I think you should be able to prove the result if you know what the poly is.Ah I see there, well you just posted the solution for Step 1, if I get rid of the strength of the assumption and loosen it up is it correct?
EDIT: And I am guessing that:
??
Re: HSC 2013 4U Marathon
Google taylor polynomials.Ah I see there, well you just posted the solution for Step 1, if I get rid of the strength of the assumption and loosen it up is it correct?
EDIT: And I am guessing that:
??
Re: HSC 2013 4U Marathon
But solution too horrendous to type out in LaTeX.
Done it!
==========
Is latex broken or something?
But solution too horrendous to type out in LaTeX.
Synchronised
Member
Re: HSC 2013 4U Marathon
Can you guys please post some difficult integration and conics questions?
Can you guys please post some difficult integration and conics questions?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Just the main points will do, and like a one sentence explanation between each 'major' line of working (i.e. skip the non important algebra)Done it!
But solution too horrendous to type out in LaTeX.
deswa1
Well-Known Member
- Joined
- Jul 12, 2011
- Messages
- 2,251
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
I haven't done it but iirc, this was a question in a Grammar paper a while ago and the easiest way to do it was to take logs of both sides and then differentiate implicitly.Just the main points will do, and like a one sentence explanation between each 'major' line of working (i.e. skip the non important algebra)
Re: HSC 2013 4U Marathon
Steps:
1. - differentiate both sides wrt x
2. - expand as required & simplify
3. - express dy/dx as approp fraction
4. - multiply numerator and denominator of said fraction by: xy(x+y)
5. - replace (x+y)n with xmyn
6. - simplify, then factorise and simplify further
7. - voila
Using logs lots easier. See below.
Basically using implicit differentiation.Just the main points will do, and like a one sentence explanation between each 'major' line of working (i.e. skip the non important algebra)
Steps:
1. - differentiate both sides wrt x
2. - expand as required & simplify
3. - express dy/dx as approp fraction
4. - multiply numerator and denominator of said fraction by: xy(x+y)
5. - replace (x+y)n with xmyn
6. - simplify, then factorise and simplify further
7. - voila
Using logs lots easier. See below.
Last edited:
Re: HSC 2013 4U Marathon
Using logs, as suggested by deswa1, is heaps easier:
ln(LHS) = ln(RHS)
mlnx + nlny = (m+n)ln(x+y)
.: m/x + n/y . dy/dx = (m+n)/(x+y) .(1+dy/dx)
.: ((m+n)/(x+y) - n/y) . dy/dx = m/x - (m+n)/(x+y)
.: dy/dx = []/[] = [m(x+y)-(m+n)x]/[(m+n)y - n(x+y)] . y/x = y/x
Using logs, as suggested by deswa1, is heaps easier:
ln(LHS) = ln(RHS)
mlnx + nlny = (m+n)ln(x+y)
.: m/x + n/y . dy/dx = (m+n)/(x+y) .(1+dy/dx)
.: ((m+n)/(x+y) - n/y) . dy/dx = m/x - (m+n)/(x+y)
.: dy/dx = []/[] = [m(x+y)-(m+n)x]/[(m+n)y - n(x+y)] . y/x = y/x
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Can you guys please post some difficult integration and conics questions?
I haven't learnt conics yet but this was on the second page (and no one answered all of it yet)
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,467
- Gender
- Undisclosed
- HSC
- N/A
Re: HSC 2013 4U Marathon
Did you mean the length of the tangent cut off by the coordinate axes?

Note, replace the 1 with a. The image in the graph sets a=1
 \ \ \ $cut off by the co-ordinate axes is of constant value$ )
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Yes, edited now.Did you mean the length of the tangent cut off by the coordinate axes?
- Status
- Not open for further replies.

