Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Lieutenant_21
Member
Re: HSC 2013 4U Marathon
Do you guys like conics? I find it extremely boring
Do you guys like conics? I find it extremely boring
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
Conics is quite bland I find... The proof of certain properties are memory based (some only, don't jump on me). Also there aren't that many applications nowadays and it isn't explored in depth in university so it has a lot less motivation than perhaps complex numbers or polynomials (and calculus )
)
Conics is quite bland I find... The proof of certain properties are memory based (some only, don't jump on me). Also there aren't that many applications nowadays and it isn't explored in depth in university so it has a lot less motivation than perhaps complex numbers or polynomials (and calculus
Lieutenant_21
Member
Re: HSC 2013 4U Marathon

^{2}=1)


Last edited:
SpiralFlex
Well-Known Member
- Joined
- Dec 18, 2010
- Messages
- 6,954
- Gender
- Female
- HSC
- N/A
Re: HSC 2013 4U Marathon
Conic sections is a beautiful topic
Conic sections is a beautiful topic
Lieutenant_21
Member
Re: HSC 2013 4U Marathon

I wish they put Real Analysis as a topic and remove conicsConics is quite bland I find... The proof of certain properties are memory based (some only, don't jump on me). Also there aren't that many applications nowadays and it isn't explored in depth in university so it has a lot less motivation than perhaps complex numbers or polynomials (and calculus)
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
It's boring because of the questions, not because of the topic. They could make more interesting questions and it would be a very nice topic.Do you guys like conics? I find it extremely boring
hayabusaboston
Well-Known Member
Re: HSC 2013 4U Marathon
wtf guys, conics is awesome! Probably one of the easiest topics in MX2 imo, and a lot of fun!
I find polynomials pree boring, complex numbers was very fun, and will be doing integration then curve sketching soon.
wtf guys, conics is awesome! Probably one of the easiest topics in MX2 imo, and a lot of fun!
I find polynomials pree boring, complex numbers was very fun, and will be doing integration then curve sketching soon.
Lieutenant_21
Member
Re: HSC 2013 4U Marathon
Polynomials is considered to be one of the simplest topics by most school teachers but the questions can get very difficult and interesting. Most school teachers go over relation between roots and roots of multiplicity which are very simple and leave out the hard end...
Conics is a cool topic but in my opinion it is the most boring topic compared to the rest of MX2 topics.wtf guys, conics is awesome! Probably one of the easiest topics in MX2 imo, and a lot of fun!
I find polynomials pree boring, complex numbers was very fun, and will be doing integration then curve sketching soon.
Polynomials is considered to be one of the simplest topics by most school teachers but the questions can get very difficult and interesting. Most school teachers go over relation between roots and roots of multiplicity which are very simple and leave out the hard end...
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon



Now notice that the function:=x^2+(4x^3-3x)^2 = f(-x) )
So its an even function, hence the roots are opposites of each other.
So I will only take one of the above cases, namely:

 )
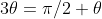

 is hence a solution
is hence a solution
 (pm there for the extra solution)
(pm there for the extra solution)
 )

Hence those are the 6 solutions. Note how I skipped some cases for the pm and stuff only because they will just give the same answers that I have before.
There is probably a much easier way to do this question, and that I did it the long way, but oh well.
Now notice that the function:
So its an even function, hence the roots are opposites of each other.
So I will only take one of the above cases, namely:
Hence those are the 6 solutions. Note how I skipped some cases for the pm and stuff only because they will just give the same answers that I have before.
There is probably a much easier way to do this question, and that I did it the long way, but oh well.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
ii) and iii)
= 0z^0 + 1z + \sum_{k=2}^{\infty} F_k z^k = z + z\sum_{k=2}^{\infty} F_{k-1}z^{k-1} + z^2 \sum_{k=2}^{\infty} F_{k-2}z^{k-2} )
 = z+z(F(z)-0z^0) + z^2(F(z)) )
(z^2+z-1) )
=\frac{-z}{z^2+z-1} )
iv) To find alpha and beta just solve the quadratic, to get A and B, just do common denominator and simultaneously solve for A and B. It is a long process, the end yields something hidden within my notes and I can't be bothered doing it again:
v)
Note how:
 = A \left(1+\frac{z}{\alpha}+\frac{z^2+}{\alpha^2})+ \dots \right) + B\left(1+\frac{z}{\beta}+\frac{z^2}{\beta^2}+ \dots \right) )
To find F_k we must equate the co-efficient of z^k on both sides

Now, just sub in alpha, beta, A and B, rationalise denominators and some arithmetic, it should yield the final result.
======================================================
As for conics, I find it a little dry considering there are no advanced conics and the questions are relatively simple. i.e. no rotated ellipses hyperbola etc.
But its a pretty good topic in my opinion (and in spirit I made a question for it)

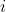 Show that the focii are$ \ \ \ S(\pm a\sqrt{2} , 0) \\ \\ $and the directrices are$ \ \ \ x=\pm \frac{a}{\sqrt{2}} \ \ \ \fbox{1} )
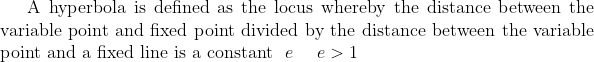
 Considering the circles$ \ \ \ x^2+y^2 = 2a^2 \ \ \ \ x^2+y^2 = \frac{a^2}{2} \ \ \ $or otherwise$)


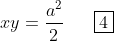
i) 0, 1, 1, 2, 3, 5, 8
ii) and iii)
iv) To find alpha and beta just solve the quadratic, to get A and B, just do common denominator and simultaneously solve for A and B. It is a long process, the end yields something hidden within my notes and I can't be bothered doing it again:
v)
Note how:
To find F_k we must equate the co-efficient of z^k on both sides
Now, just sub in alpha, beta, A and B, rationalise denominators and some arithmetic, it should yield the final result.
======================================================
As for conics, I find it a little dry considering there are no advanced conics and the questions are relatively simple. i.e. no rotated ellipses hyperbola etc.
But its a pretty good topic in my opinion (and in spirit I made a question for it)
Last edited:
Re: HSC 2013 4U Marathon
This can also be proved using mappings in complex numbers/analysis.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
EDIT: I did it and it is still applicable to use complex numbers by simply using x+iy (disregard the above part)
But the question still stands lol
This is true (as had been demonstrated previous pages back) but I'm pretty sure the parametric equations of a hyperbola are out of syllabus (hyperbolic sine and cosine).This can also be proved using mappings in complex numbers/analysis.
EDIT: I did it and it is still applicable to use complex numbers by simply using x+iy (disregard the above part)
But the question still stands lol
Last edited:
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
, (1 - z_2), \dots , (1 - z_{n-1})$ $ is n ($ $ where n is even))
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

Note that:

In this case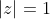
The constant term is:
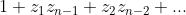


The roots occur in conjugate pairs, that is:
Note that:
In this case
The constant term is:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,219
- Gender
- Undisclosed
- HSC
- 2012
Re: HSC 2013 4U Marathon
Wouldn't there be n/2 pairs of roots...?The roots occur in conjugate pairs, that is:
Note that:
In this case
The constant term is:

Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
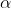 be a root of z^n-1=0
be a root of z^n-1=0
Lets form a polynomial with roots, 1-1, 1-z_1, 1-z_2, ....

Therefore the polynomial with roots:
, (1-z_2) ... , (1-z_{n-1}) )
is
^n - 1 = 0 )
^{n-1} n z = 0 )
Now we will eliminate one solution, namely 0, or 1-1

The above equation has roots (1-z_1), (1-z_2), .... , (1-z_(n-1))
The constant term is -n ??
let
Lets form a polynomial with roots, 1-1, 1-z_1, 1-z_2, ....
Therefore the polynomial with roots:
is
Now we will eliminate one solution, namely 0, or 1-1
The above equation has roots (1-z_1), (1-z_2), .... , (1-z_(n-1))
The constant term is -n ??
Re: HSC 2013 4U Marathon
I personally enjoy conics :LDo you guys like conics? I find it extremely boring
- Status
- Not open for further replies.

