HSC 2013 MX2 Marathon (archive) (5 Viewers)

twinklegal19 · Apr 13, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
I don't think so, but I think its a bit unreasonable of me to ask it like that with no hint whatsoever.

Redone:

$$Find, using the substitution$ \ \ t=\tan \frac{x}{2}$

$\int \frac{1-t^2}{1+10t^2+t^4} \ dt$

ah, I did it without substitution by completing the square and converting to partial fractions. It should be able to be integated into inverse tans ?
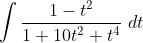
dunno if it works lol

$\frac{1-2\sqrt{6}}{4\sqrt{30-12\sqrt{6}}}\tan^{-1}{\frac{t}{\sqrt{5-2\sqrt{6}}}}-\frac{1+2\sqrt{6}}{4\sqrt{30+12\sqrt{6}}}\tan^{-1}{\frac{t}{\sqrt{5+2\sqrt{6}}}}+$C$$

I probably made an error somewhere

asianese · Apr 13, 2013

Re: HSC 2013 4U Marathon

The integral is possible through completing the square and then doing a partial fractions.

Did you mean x=tan(t/2) by any off chance?

Sy123 · Apr 13, 2013

Re: HSC 2013 4U Marathon

asianese said:
The integral is possible through completing the square and then doing a partial fractions.

Did you mean x=tan(t/2) by any off chance?

Nah definitely t=tan(x/2)
I intended the person to go backwards with it, i.e. notice that the denominator is actually

$(t^2+1)^2 + 8t^2$

With some manipulation thereon, it returns that, the integrand:

$\frac{1-t^2}{1+10t^2+t^4} = \frac{\frac{1-t^2}{1+t^2} \cdot \frac{1}{1+t^2}}{1+ 2\frac{4t^2}{(1+t^2)^2}}$

We notice that we can sub in various trigonometric equations into there, including a dx, cos x, and sin^2 x

Then integrate normally as it is in tan^-1 form.

===================

This is a really good question:

Sy123 · Apr 13, 2013

Re: HSC 2013 4U Marathon

$Evaluate$

$I= \int_0^1 x^3 \tan^{-1} \left (\frac{1-x}{1+x} \right ) \ dx$

HeroicPandas · Apr 14, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$Evaluate$

$I= \int_0^1 x^3 \tan^{-1} \left (\frac{1-x}{1+x} \right ) \ dx$

I got

$I = \frac{1}{4} [\frac{\pi}{4} - \frac{2}{3}]$

By integration by parts: (u = arctan...., dv = x^3...)

$I = \left [ \frac{x^4}{4} tan^{-1} \frac{1-x}{1+x} \right ]^1 _0 - \frac{1}{4} \int_{0}^{1} x^4 . \frac{-2}{(1+x)^2 + (1-x)^2}$

$I = \frac{1}{4} \int_{0}^{1} \frac{x^4 .dx }{1 + x^2} = \frac{1}{4} \int_{0}^{1} (\frac{x^4 - 1 }{1+x^2}- \frac{1}{1+x^2}).dx = \frac{1}{4} \int_{0}^{1} (x^2 - 1 - \frac{1}{1+x^2}).dx$

Therefore,

$I = \frac{1}{4} [\frac{\pi}{4} - \frac{2}{3}]$

Sy123 · Apr 14, 2013

Re: HSC 2013 4U Marathon

HeroicPandas said:
I got

$I = \frac{1}{4} [\frac{\pi}{4} - \frac{2}{3}]$

By integration by parts: (u = arctan...., dv = x^3...)

$I = \left [ \frac{x^4}{4} tan^{-1} \frac{1-x}{1+x} \right ]^1 _0 - \frac{1}{4} \int_{0}^{1} x^4 . \frac{-2}{(1+x)^2 + (1-x)^2}$

$I = \frac{1}{4} \int_{0}^{1} \frac{x^4 .dx }{1 + x^2} = \frac{1}{4} \int_{0}^{1} (\frac{x^4 - 1 }{1+x^2}- \frac{1}{1+x^2}).dx = \frac{1}{4} \int_{0}^{1} (x^2 - 1 - \frac{1}{1+x^2}).dx$

Therefore,

$I = \frac{1}{4} [\frac{\pi}{4} - \frac{2}{3}]$

Yep something like that, nice work.

HeroicPandas · Apr 14, 2013

Re: HSC 2013 4U Marathon

Problème

$$ Find $\int \frac{ \sin2x}{(1+\sin^2x)^2} dx$

Sy123 · Apr 14, 2013

Re: HSC 2013 4U Marathon

HeroicPandas said:
Problème

$$ Find $\int \frac{ \sin2x}{(1+\sin^2x)^2} dx$

$I= \int \frac{ \sin2x}{(1+\sin^2x)^2} \ dx$

$$let$ \ \ u =\sin^2 x$

$du=\sin(2x) \ dx$

$\therefore \ \ I = \int \frac{du}{(1+u)^2} = \frac{-1}{1+u} + c$

$\therefore \ \ I = \frac{-1}{1+\sin^2 x} + c$

twinklegal19 · Apr 14, 2013

Re: HSC 2013 4U Marathon

HeroicPandas said:
Problème

$$ Find $\int \frac{ \sin2x}{(1+\sin^2x)^2} dx$

$\begin{align*}\int \frac{\sin2x}{(1+\sin^2x)^2}dx&=\int \frac{ 2\sin{x}\cos{x}}{(1+\sin^2x)^2}dx\\&=\int \frac{ d\left ( \sin^2{x} \right )}{(1+\sin^2x)^2}\\&=-\frac{1}{\left ( 1+\sin^2x\right )}+C\end{align*}$

edit: lol sy beat me to it

HeroicPandas · Apr 14, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$I= \int \frac{ \sin2x}{(1+\sin^2x)^2} \ dx$

$$let$ \ \ u =\sin^2 x$

$du=\sin(2x) \ dx$

$\therefore \ \ I = \int \frac{du}{(1+u)^2} = \frac{-1}{1+u} + c$

$\therefore \ \ I = \frac{-1}{1+\sin^2 x} + c$

Noice

twinklegal19 said:
$\begin{align*}\int \frac{\sin2x}{(1+\sin^2x)^2}&=\int \frac{ 2\sin{x}\cos{x}}{(1+\sin^2x)^2}\\&=\int \frac{ d\left ( \sin^2{x} \right )}{(1+\sin^2x)^2}\\&=-\frac{1}{\left ( 1+\sin^2x\right )}+C\end{align*}$

edit: lol sy beat me to it

Noice

Sy123 · Apr 14, 2013

Re: HSC 2013 4U Marathon

$Consider the tetrahedron shown in the diagram$

$$With side lengths$ \ \ OA = a \ \ OB = b \ \ OC = c$

$$Moreover, the perpendicular from$ \ \ O \ \ $to$ \ \ \triangle ABC \ \ $has length$ \ \ d$

$By considering the volume of the tetrahedron$

$Prove that$

$\frac{1}{d^2} = \frac{1}{a^2} + \frac{1}{b^2} + \frac{1}{c^2}$

Sy123 · Apr 14, 2013

Re: HSC 2013 4U Marathon

$Find$

$\int \frac{dx}{(x+2)\sqrt{x^2+4x-5}}$

twinklegal19 · Apr 15, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$Find$

$\int \frac{dx}{(x+2)\sqrt{x^2+4x-5}}$

$\begin{align*}I&=\int \frac{dx}{(x+2)\sqrt{x^2+4x-5}}\\u^2&=x^2+4x-5\\&=(x+2)^2-9\\u^2+9&=(x+2)^2\\dx&=u\frac{du}{x+2}\\I&=\int \frac{u\cdot du}{(x+2)^2u}\\&=\int \frac{du}{u^2+9}\\&=\frac{1}{3}\tan^{-1}\left ( \frac{\sqrt{x^2+4x-5}}{3} \right )+C\end{align*}$

seanieg89 · Apr 15, 2013

Re: HSC 2013 4U Marathon

A lattice point is a point in the cartesian plane with integer coordinates.

Prove by induction or otherwise that the area of a polygon in the cartesian plane with vertices on lattice points is given by:

{Number of lattice points strictly inside P} - {Number of lattice points lying on the boundary of P}/2 - 1.

Difficulty: 2/5.

RealiseNothing · Apr 15, 2013

Re: HSC 2013 4U Marathon

Here's a very nice question (imo) that I just came up with after an idea popped into my head last night.

i) Explain why:

$\frac{(\pi-2x)sinx}{(\pi-x)x}$

Is well defined for $x \to 0$

ii) Now integrate:

$\int_{0}^{\pi} \frac{(\pi-2x)sinx}{(\pi-x)x} dx$

seanieg89 · Apr 15, 2013

Re: HSC 2013 4U Marathon

RealiseNothing said:
Here's a very nice question (imo) that I just came up with after an idea popped into my head last night.

i) Explain why:

$\frac{(\pi-2x)sinx}{(\pi-x)x}$

Is well defined for $x \to 0$

ii) Now integrate:

$\int_{0}^{\pi} \frac{(\pi-2x)sinx}{(\pi-x)x} dx$

1. Because sin(x) is asymptotically equivalent to x as x - > 0, as is assumed without proof in the mx2 syllabus. Similarly sin(x)/(pi-x) tends to 1 as x - > pi.

2. 0. Simply apply the rule:

$\int_0^a f(x)\,dx =\int_0^a f(a-x)\, dx$

and the result is immediate, as the integrand simply changes sign.

seanieg89 · Apr 15, 2013

Re: HSC 2013 4U Marathon

In the following question you may assume without proof that if a continuous function f is positive at some c, then there is a small interval centred at c in which f > f(c)/2.

0. Prove that a non-negative continuous function with integral 0 over some interval of positive length must be 0 everywhere on the interval.

1. Fix real numbers a and b with a < b.

Prove that the only function g which satisfies:

g has a continuous second derivative on the interval [a,b],

g(a)=g(b)=0,

g''g >= 0 on the interval [a,b],

is zero identically on the interval [a,b].

2. Hence deduce that for any function f with f'' > 0 on the interval [a,b], and for any x1,x2,...,xn in [a,b] we have:

$\sum_{j=1}^n \lambda_jf(x_j)\geq f\left(\sum_{j=1}^n \lambda_jx_j\right)$

where the $\lambda_j$ 's are arbitrary real numbers such that

$0\leq \lambda_j \leq 1,\sum_j \lambda_j=1$ .

Interpret this result geometrically.

3. By considering the function log(x) and using the result from 2, prove the inequality:

$\sum_{j=1}^n \lambda_j x_j\right \geq \prod_{j=1}^n x_j^{\lambda_j}$

for positive $x_j$ and $\lambda_j$ as in 2. What familiar result does this become if we take every $\lambda_j$ to be 1/n?

4. There are n guards each to be stationed 1 km away from a government building. Each one can see everything within a radius of 1km from himself. Using the result proven in 2., find the maximum possible area that n guards can cover.

Difficulty: 4/5.

seanieg89 · Apr 15, 2013

Re: HSC 2013 4U Marathon

seanieg89 said:
$In this question you may assume:\\ Let $(a_j)$ be a sequence of complex numbers. If there exists an $M>0$ such that:\\ \\ $\sum_{j=0}^n |a_j|\leq M$\\ \\ for all $n$, then the series\\ $\sum_{j=0}^\infty a_j$\\ converges. \\ \\ \\ Let $(a_n)$ be a positive and decreasing sequence with $a_n\rightarrow 0$. Prove that $\sum_{n=0}^\infty a_n$ does not necessarily have to converge, but $\sum_{n=0}^\infty a_n\cos(n\theta)$ converges for every $\theta$ not divisible by $2\pi$. Are all of our conditions on the sequence $a$ necessary for this result to hold?$

Difficulty rating: 4/5.

bumpage.

seanieg89 · Apr 15, 2013

Re: HSC 2013 4U Marathon

seanieg89 said:
$Given two polynomials $p(z)$, $d(z)$ with complex coefficients prove that there exist unique polynomials $q(z)$ and $r(z)$ such that: \\ \\$p(z)=q(z)d(z)+r(z)$ \\and $\deg(r)<\deg(d)$. \\ \\(Note that by convention, $\deg(0):=-\infty$.)$

bump.

Difficulty: 1.5/5.

seanieg89 · Apr 15, 2013

Re: HSC 2013 4U Marathon

seanieg89 said:
$Find the minimum possible value of $a^2+b^2$ where $a$ and $b$ are two real numbers such that the polynomial:\\ \\ $x^4+ax^3+bx^2+ax+1$\\ \\ has at least one real root.$

bump.

Difficulty: 3.14159/5

That should be enough to keep 2013'ers busy for a while.

HSC 2013 MX2 Marathon (archive) (5 Viewers)

.

Σ

This too shall pass

This too shall pass

Heroic!

This too shall pass

Heroic!

This too shall pass

.

Heroic!

This too shall pass

This too shall pass

.

Well-Known Member

what is that?It is Cowpea

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 5)