Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon


HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
let x^2 = tanθ
2x.dx = sec^2 θ .dθ
When x= 0, θ = 0
When x = INFTY, θ = pi/2
therefore, int(θ=0 to θ=pi/2) = 0.5 dθ
therefore, I = pi/4?
Let integral be I
let x^2 = tanθ
2x.dx = sec^2 θ .dθ
When x= 0, θ = 0
When x = INFTY, θ = pi/2
therefore, int(θ=0 to θ=pi/2) = 0.5 dθ
therefore, I = pi/4?
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
You have made a mistake when subbing dx back into the integralLet integral be I
let x^2 = tanθ
2x.dx = sec^2 θ .dθ
When x= 0, θ = 0
When x = INFTY, θ = pi/2
therefore, int(θ=0 to θ=pi/2) = 0.5 dθ
therefore, I = pi/4?
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
The only substitution you can use is x=tanx; which doesn't really help.
which doesn't really help.
You can't use that substitution because you can't get rid off the x after you sub dx back.Let integral be I
let x^2 = tanθ
2x.dx = sec^2 θ .dθ
When x= 0, θ = 0
When x = INFTY, θ = pi/2
therefore, int(θ=0 to θ=pi/2) = 0.5 dθ
therefore, I = pi/4?
The only substitution you can use is x=tanx;
Last edited:
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
This can be so easily done using abstract algebra but I don't think that is HSC level.
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
The final result is nice though. Allows you to evaluate a sine Fresnel Integral without using complex analysis (you need Gamma function though).Hint: fugly completion of squares
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
 )
By integrating both sides, we yield:
First and second fractions are logarithms, both elements inside the logarithm functions are monic quadratics, at infinity they cancel to 1, making the first 2 terms together 0, at x=0, the same happens and we get the logarithm of 1 which is again zero.
The second 2 terms are in the form for the atan function. After completing the square and manipulations, we evaluate them at infinity keeping in mind that at infinity atan is pi/2.
In the end we should arrive at

Also it would be awesome if people started posting these integrals in the integration marathon please =)
Finding roots of unity then expressing in quadratic factors then applying partial fractions, then manipulating to get it into a suitable integral form:
By integrating both sides, we yield:
First and second fractions are logarithms, both elements inside the logarithm functions are monic quadratics, at infinity they cancel to 1, making the first 2 terms together 0, at x=0, the same happens and we get the logarithm of 1 which is again zero.
The second 2 terms are in the form for the atan function. After completing the square and manipulations, we evaluate them at infinity keeping in mind that at infinity atan is pi/2.
In the end we should arrive at
Also it would be awesome if people started posting these integrals in the integration marathon please =)
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
By the way,dx=\frac{1}{\sqrt{\pi }}\int_{0}^{\infty }\frac{1}{x^{4}+1}dx=\frac{\sqrt{\pi} }{2\sqrt{2}} )
No problem, I will post there next time.
Good job!Finding roots of unity then expressing in quadratic factors then applying partial fractions, then manipulating to get it into a suitable integral form:
By integrating both sides, we yield:
First and second fractions are logarithms, both elements inside the logarithm functions are monic quadratics, at infinity they cancel to 1, making the first 2 terms together 0, at x=0, the same happens and we get the logarithm of 1 which is again zero.
The second 2 terms are in the form for the atan function. After completing the square and manipulations, we evaluate them at infinity keeping in mind that at infinity atan is pi/2.
In the end we should arrive at
Also it would be awesome if people started posting these integrals in the integration marathon please =)
By the way,
No problem, I will post there next time.
HeroicPandas
Heroic!
- Joined
- Mar 8, 2012
- Messages
- 1,546
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
ahh yes lol, thanksYou have made a mistake when subbing dx back into the integral
ah yes i see thanksYou can't use that substitution because you can't get rid off the x after you sub dx back.
The only substitution you can use is x=tanx;which doesn't really help.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
No heavy machinery required here, the simplest proof of this fact that I can think of is essentially identical to the standard proof of a course theorem.This can be so easily done using abstract algebra but I don't think that is HSC level.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
In this question you may assume that:
 = \sum_0^{\infty} (-1)^k \frac{x^{2k}}{(2k)!})
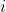 Explain why the polynomial$)
 = \frac{(x-a)(x-b)(x-c)(x-d)}{abcd})
=1)
 Show that$)
 = (1-\frac{x}{a})(1-\frac{x}{b})(1-\frac{x}{c})(1-\frac{x}{d}))
 Assuming the result in part (ii) holds for polynomials of infinite degree, prove that$)
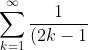^2} = \frac{\pi^2}{8})
In this question you may assume that:
Last edited:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
I know haha, but proving those assumptions is a little beyond MX2, so I let people assume it.Lol rather large assumptions there Realise.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

Plus Euler assumed them, why can't weLol rather large assumptions there Realise.
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
Re: HSC 2013 4U Marathon
He eventually found a rigorous proof. You actually need quite a lot of machinery to make that particular proof work (much more than you have stated I am pretty sure).
Edit: To be a little more concrete in my criticism, my main objection is that it is not at all clear that the symmetric polynomials in the roots of a power series have to be related to the coefficients of the power series in the same way that is true of polynomials. (In fact this is not true in general.)
To make this argument work we need to assume something along the lines of the Weierstrass factorisation theorem, as well as some facts about convergence and uniform convergence. In short, I think that this isn't a good choice for an MX2 question because I think it is better for the assumptions to be milder and more precise. That way, the student is at least engaging in (close-to) rigorous mathematical reasoning just skipping the theory leading up to the assumption rather than doing a whole series of hand-wavy steps.
He eventually found a rigorous proof. You actually need quite a lot of machinery to make that particular proof work (much more than you have stated I am pretty sure).
Edit: To be a little more concrete in my criticism, my main objection is that it is not at all clear that the symmetric polynomials in the roots of a power series have to be related to the coefficients of the power series in the same way that is true of polynomials. (In fact this is not true in general.)
To make this argument work we need to assume something along the lines of the Weierstrass factorisation theorem, as well as some facts about convergence and uniform convergence. In short, I think that this isn't a good choice for an MX2 question because I think it is better for the assumptions to be milder and more precise. That way, the student is at least engaging in (close-to) rigorous mathematical reasoning just skipping the theory leading up to the assumption rather than doing a whole series of hand-wavy steps.
Last edited:
Registered User
Member
- Joined
- May 4, 2013
- Messages
- 110
- Gender
- Male
- HSC
- N/A
Re: HSC 2013 4U Marathon
Do you do this questions using the conjugate root theorem?
- Status
- Not open for further replies.

