HSC 2013 MX2 Marathon (archive) (1 Viewer)

RealiseNothing · May 8, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
The problem simply boils down to computing:

$P = \sum_{k=0}^{m} \binom{n+k}{n} (P(T))^n (P(H))^k$

$\frac{1-P(H)}{P(H)} = q \ \ P(H) = \frac{1}{q+1} \ \ P(T) = \frac{q}{q+1}$

Is it possible to compute

$\sum_{k=0}^{m} \binom{n+k}{k} x^k$

? Its easy if x is 1 but....

$\sum_{k=0}^{m}\binom{n+k}{k}x^k = \frac{1}{(1-x)^{n+1}}$

Wait, this is only for $m \to \infty$

hayabusaboston · May 8, 2013

Re: HSC 2013 4U Marathon

how the eff do u guys type up latex so quick?

srsly

I tried to use it once and thought nah

too much stuff.

But hey I guess u get used to it.

RealiseNothing · May 8, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
The problem simply boils down to computing:

$P = \sum_{k=0}^{m} \binom{n+k}{n} (P(T))^n (P(H))^k$

$\frac{1-P(H)}{P(H)} = q \ \ P(H) = \frac{1}{q+1} \ \ P(T) = \frac{q}{q+1}$

Is it possible to compute

$\sum_{k=0}^{m} \binom{n+k}{k} x^k$

? Its easy if x is 1 but....

The good thing about this, is that if we do solve this question using a different method (I have a different one in mind), then since we know the answer, we could probably use it to find the above summation.

Sy123 · May 8, 2013

Re: HSC 2013 4U Marathon

RealiseNothing said:
The good thing about this, is that if we do solve this question using a different method (I have a different one in mind), then since we know the answer, we could probably use it to find the above summation.

That is true.

RealiseNothing · May 8, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
That is true.

I have a solution, but I'll wait and see if anyone else posts one so I can compare, since I'm not 100% sure yet, still trying to see if everything works the way I think it should.

RealiseNothing · May 8, 2013

Re: HSC 2013 4U Marathon

May as well just post what my answer is atm, still checking it though. Will post my method if it is confirmed correct:

$\frac{qm}{qm+n}$

asianese · May 8, 2013

Re: HSC 2013 4U Marathon

hayabusaboston said:
how the eff do u guys type up latex so quick?

srsly

I tried to use it once and thought nah

too much stuff.

But hey I guess u get used to it.

It is helpful if you are fast at typing to begin with. Around 100wpm is a good speed. Then once you get used to the commands, backslashes, braces and all it becomes quite natural. What I normally do is think of what I'm trying to type in my head and it should 'flow' into your fingers as you garnish your thoughts with word wraps and backslashes and formatting.

RealiseNothing · May 8, 2013

Re: HSC 2013 4U Marathon

RealiseNothing said:
May as well just post what my answer is atm, still checking it though. Will post my method if it is confirmed correct:

$\frac{qm}{qm+n}$

Yer I don't think this is right, it seems to work for some cases but not all. Going to try and adjust my method a bit to work for all cases.

hayabusaboston · May 8, 2013

Re: HSC 2013 4U Marathon

asianese said:
It is helpful if you are fast at typing to begin with. Around 100wpm is a good speed. Then once you get used to the commands, backslashes, braces and all it becomes quite natural. What I normally do is think of what I'm trying to type in my head and it should 'flow' into your fingers as you garnish your thoughts with word wraps and backslashes and formatting.

I can type 100 words per minute when im focused on something lol.

But latex seems so... boring to use I guess. But it makes things simpler and much more clear definitely, so I suppose its worth it learning how to use it.

asianese · May 8, 2013

Re: HSC 2013 4U Marathon

Only bother learning it if you are seriously considering continuing on with mathematics..

That is, if you are busy. If you have spare time then go for it. lol

Carrotsticks · May 8, 2013

Re: HSC 2013 4U Marathon

asianese said:
Only bother learning it if you are seriously considering continuing on with mathematics..

That is, if you are busy. If you have spare time then go for it. lol

Not necessarily. A lot of reports involving statistics (such as graduate Biology papers) are also compiled in TeX.

Registered User · May 8, 2013

Re: HSC 2013 4U Marathon

A rectangle is drawn where the lengths of the sides are chosen randomly from [0, 10] and independently of one another. Find the probability that the length of its diagonal is smaller than or equal to 10.

Carrotsticks · May 8, 2013

Re: HSC 2013 4U Marathon

Registered User said:
A rectangle is drawn where the lengths of the sides are chosen randomly from [0, 10] and independently of one another. Find the probability that the length of its diagonal is smaller than or equal to 10.

Geometric probability is straying quite a bit from Extension 2 without any prior intuition. Not many students fully grasp the concept of probability being the area under a curve.

RealiseNothing · May 8, 2013

Re: HSC 2013 4U Marathon

Carrotsticks said:
Geometric probability is straying quite a bit from Extension 2 without any prior intuition. Not many students fully grasp the concept of probability being the area under a curve.

That's what I'm using for my probability question (the m heads before n tails one).

seanieg89 · May 8, 2013

Re: HSC 2013 4U Marathon

Am disappointed that no-one has answered Sy's conjugate root question!

Trebla · May 9, 2013

Re: HSC 2013 4U Marathon

hayabusaboston said:
I can type 100 words per minute when im focused on something lol.

But latex seems so... boring to use I guess. But it makes things simpler and much more clear definitely, so I suppose its worth it learning how to use it.

Like any coding, LaTeX is incredibly annoying to learn at first but once you're familiar with it most of the things will come naturally. I was forced to get used to it because I needed it to write a 70 page thesis.

Sy123 · May 9, 2013

Re: HSC 2013 4U Marathon

Registered User said:
A rectangle is drawn where the lengths of the sides are chosen randomly from [0, 10] and independently of one another. Find the probability that the length of its diagonal is smaller than or equal to 10.

Hopefully this is correct.

Varying the sides of lengths x and y, then the curve represented by the length of the diagonal is $x^2 + y^2 \leq 100$ x > 0 y > 0
Therefore the probability is that area that satisfies the above equation, divided by the square 10 x 10 since that represents all the choices.

Therefore it is: $\pi (10)^2/4 \div 100 = \pi/4$

Sy123 · May 9, 2013

Re: HSC 2013 4U Marathon

seanieg89 said:
Am disappointed that no-one has answered Sy's conjugate root question!

Can you please criticise this proof? I am starting to have doubts about it.

===

Start with the polynomial,

$x=p+\sqrt{q}$

We need to make the lowest reducible rational polynomial that has that as a root, so we simply:

$(x-p)^2 - q = 0$

The above polynomial has the root $p - \sqrt{q}$
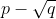
It is the simplest most reducible rational polynomial that has p + root(q) as a root.

Now consider:

$P(x) = a_1(x) a_2(x) \dots a_n(x)$

Where a_1, a_2 ... are all rational polynomial functions of lowest reducibility.

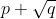
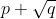
If $p+\sqrt{q}$ is a root then among the series a_1, a_2... there must exist a_k for some k such that $p+\sqrt{q}$ is a root.
Since a_k is irreducible and rational, then that polynomial must be:

$a_k(x) = (x-p)^2 - q$

And that polynomial also has the root $p-\sqrt{q}$

Therefore that is also a root of P(x).
Is there a gap or something in this? Or is it all good?

Registered User · May 9, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
Hopefully this is correct.

Varying the sides of lengths x and y, then the curve represented by the length of the diagonal is $x^2 + y^2 \leq 100$ x > 0 y > 0
Therefore the probability is that area that satisfies the above equation, divided by the square 10 x 10 since that represents all the choices.

Therefore it is: $\pi (10)^2/4 \div 100 = \pi/4$

That is correct. Good job.

Registered User · May 9, 2013

Re: HSC 2013 4U Marathon

Sy123 said:
$Prove that$

$\sum_{n=1}^{\infty} \frac{\sin(n\theta)}{n} = \frac{\pi}{2} - \frac{\theta}{2} \ \ \ \ \ \fbox{7}$

$0 \leq \theta \leq 2\pi$

In this proof I will assume that $x -\frac{x^2}{2}+\frac{x^3}{3}\cdots$ converges to $\ln (1+x)$ (Taylor Series).
$Let,$

$S_1 = \sum_{n=1}^{\infty}\frac{\cos n\theta}{n}$

$S_2 = \sum_{n=1}^{\infty}\frac{\sin n\theta}{n}$

$Then$ $S_1 + iS_2 = \sum_{n=1}^{\infty}\frac{\cos(n\theta)+i\sin(n \theta)}{n}=\sum_{n=1}^{\infty}\frac{e^{in\theta}}{n}$

$Now, from the Taylor expansion,$ $\ln (1+x) = x -\frac{x^2}{2}+\frac{x^3}{3}\cdots$

$\implies -\ln(1-x) = x+ \frac{x^2}{2}+\frac{x^3}{3} ... = \sum_{n=1}^{\infty}\frac{x^n}{n}$

$\therefore S_1+iS_2 = -\ln(1-e^{i\theta})$

$=-\ln(1-\cos\theta-i\sin \theta)$

$=-\ln(2\sin^2\theta/2 - 2i\sin(\theta/2)\cos(\theta/2))$

$=-\ln(2\sin\theta/2)-\ln(\sin\theta/2-i\cos\theta/2)$

$=-\ln(2\sin\theta/2)+\ln(\sin\theta/2+i\cos\theta/2)$

$=-\ln(2\sin\theta/2)+\ln(e^{i(\pi/2-\theta/2)})$

$=-\ln(2\sin\theta/2)+i(\pi/2-\theta/2)$

$Taking the imaginary part of both sides,$

$S_2 = \frac{\pi}{2} - \frac{\theta}{2}$

==================================================

$Prove that$

$\sum_{k=-\infty}^{\infty}\left(\dfrac{\sin(k)}{k}\right)^{2}=\pi$

Make a Difference – Donate to Bored of Studies!

HSC 2013 MX2 Marathon (archive) (1 Viewer)

what is that?It is Cowpea

Well-Known Member

what is that?It is Cowpea

This too shall pass

what is that?It is Cowpea

what is that?It is Cowpea

Σ

what is that?It is Cowpea

Well-Known Member

Σ

Retired

Member

Retired

what is that?It is Cowpea

Well-Known Member

Administrator

This too shall pass

This too shall pass

Member

Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)