-
Best of luck to the class of 2025 for their HSC exams. You got this! Let us know your thoughts on the HSC exams here
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2013 MX2 Marathon (archive) (1 Viewer)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
Find through differentiating that nromal to curve at A is:
x+2ay=2a^3+a
Intersection of normals at A and B are
(-2ab(a+b), a^2+ab+b^2+1/2)
Intersections of normals at A and C are
(-2ac(a+c), a^2+ac+c^2+1/2)
Equating x-y coordinates we get that a+b+c=0, hence proof is complete.
============================


Let the points be A(a,a^2), B(b,b^2), C(c,c^2)Suppose that three points on the parabola y=x^2 have the property that their normal lines intersect at a common point. Show that the sum of their x-coordinates is 0.
Find through differentiating that nromal to curve at A is:
x+2ay=2a^3+a
Intersection of normals at A and B are
(-2ab(a+b), a^2+ab+b^2+1/2)
Intersections of normals at A and C are
(-2ac(a+c), a^2+ac+c^2+1/2)
Equating x-y coordinates we get that a+b+c=0, hence proof is complete.
============================
RealiseNothing
what is that?It is Cowpea
Last edited:
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
The first inequality isn't always true for all positive integers n.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

The cases of 1, 2, 3 can just be manually tested I guess. At the time I originally had}{2}) which works for all integers, until I realised it's n-1 not n+1, and thought it still worked without actually testing it lol.
which works for all integers, until I realised it's n-1 not n+1, and thought it still worked without actually testing it lol.
It works for integersThe first inequality isn't always true for all positive integers n.
The cases of 1, 2, 3 can just be manually tested I guess. At the time I originally had
nightweaver066
Well-Known Member
- Joined
- Jul 7, 2010
- Messages
- 1,585
- Gender
- Male
- HSC
- 2012
Re: HSC 2013 4U Marathon
!2!}=\frac{n}{2}(n-1) = \frac{n}{2}(1 + n) - n = 1 + 2 + ... + (n - 1) > ln(1) + ln(2) + ... + ln(n-1) = ln((n-1)! \; (x > lnx))
!)
 so close.
so close.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
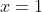 LHS=RHS
LHS=RHS
differentiating both sides gives LHS'=1 and RHS'=1/x so for x>1 LHS>RHS
then apply what nightweaver did, and the solution is done
WhenHint: first prove that for x > 1
x - 1 > ln x
then go from there
differentiating both sides gives LHS'=1 and RHS'=1/x so for x>1 LHS>RHS
then apply what nightweaver did, and the solution is done
- Joined
- Feb 16, 2005
- Messages
- 8,536
- Gender
- Male
- HSC
- 2006
Re: HSC 2013 4U Marathon
lol you can't differentiate both sides of an inequalityWhenLHS=RHS
differentiating both sides gives LHS'=1 and RHS'=1/x so for x>1 LHS>RHS
then apply what nightweaver did, and the solution is done
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
like, if you differentiate x-1 you get 1, and if you differentiate ln(x) you get 1/x, so x-1 increases faster than ln(x) for x>1, but at x=1 they are equal, thus for x>1, x-1>ln(x)
no not like thatlol you can't differentiate both sides of an inequality
like, if you differentiate x-1 you get 1, and if you differentiate ln(x) you get 1/x, so x-1 increases faster than ln(x) for x>1, but at x=1 they are equal, thus for x>1, x-1>ln(x)
- Joined
- Feb 16, 2005
- Messages
- 8,536
- Gender
- Male
- HSC
- 2006
Re: HSC 2013 4U Marathon
Oh right. I would normally just show that the maximum value of y = ln x - x is -1.no not like that
like, if you differentiate x-1 you get 1, and if you differentiate ln(x) you get 1/x, so x-1 increases faster than ln(x) for x>1, but at x=1 they are equal, thus for x>1, x-1>ln(x)
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
=====




ah ok, well done.It works for integers
The cases of 1, 2, 3 can just be manually tested I guess. At the time I originally hadwhich works for all integers, until I realised it's n-1 not n+1, and thought it still worked without actually testing it lol.
=====
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon

Now using

Therefore:



Letah ok, well done.
=====

Now using
Therefore:
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon


Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon


}{d\theta} \cdot \frac{d\theta}{dv} = \frac{d\left(\frac{1}{2}v^2 \right )}{dv} = v )
 \frac{d \theta}{dv} )
 )
b) Resolve all forces with respect to the perpendicular axes of the Tension and tangential acceleration vectors, we find that

Where a is the acceleration, the decomposed gravity vector opposes the tangential acceleration

But from part (a), = -g\sin \theta )
===========================




b) Resolve all forces with respect to the perpendicular axes of the Tension and tangential acceleration vectors, we find that
Where a is the acceleration, the decomposed gravity vector opposes the tangential acceleration
But from part (a),
===========================
Re: HSC 2013 4U Marathon
Consider the ellipse x^2/100 + y^2/25 = 1, and let P be the point (6,4) on the ellipse. If the normal at P meets the major axis at G, and OH is the perpendicular drawn from the origin to the tangent at P, show that PG x OH = 25.
Consider the ellipse x^2/100 + y^2/25 = 1, and let P be the point (6,4) on the ellipse. If the normal at P meets the major axis at G, and OH is the perpendicular drawn from the origin to the tangent at P, show that PG x OH = 25.
RealiseNothing
what is that?It is Cowpea
Re: HSC 2013 4U Marathon
Very similar to last year's BOS trial question 15 by carrot.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2013 4U Marathon
H_n - ln(n) = E_n + 1/n, so the result is practically given, for my one it is not given.
Well it is given that E_n approaches a finite limit, andVery similar to last year's BOS trial question 15 by carrot.
H_n - ln(n) = E_n + 1/n, so the result is practically given, for my one it is not given.
- Status
- Not open for further replies.

