Re: HSC 2013 4U Marathon
Here's my go at the question. I'll just do the left inequality and presume the right inequality is similar.
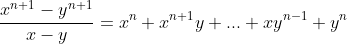
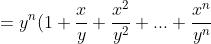>y^n(n+1))
^k>1)
Yeah I did it again and you are correct
Ah yes reading the solution again it is incorrect, what I had in mind was
... (1)
.... (2)
This is done by subbing in the AM-GM inequality, all substitutions are positive since x_k <= 1/2
Dividing (2) by (1), which we can do since all things are positive.
We get(P is what we want)
Then flip everything, when we do that the inequality sign switches, yeilding P > (that)
But I was skimming through her solution and wasn't really paying attention, which is why I couldn't see that.
=====
I'm making way too many mistakes
(there is no mistake in this one)
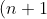y^n < \frac{x^{n+1} - y^{n+1}}{x-y} < (n+1) x^n )
Here's my go at the question. I'll just do the left inequality and presume the right inequality is similar.
