Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,725
- Gender
- Male
- HSC
- 2013
Re: HSC 2014 4U Marathon - Advanced Level
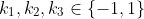
$ \\ \\ $Case 2:$ \ \ $2 of$ \ k_1, k_2, k_3 \ $is$ \ -1 \ $w.l.o.g$ \ k_1=k_2 = -1 \ , \ k_3 = 1 \\ \\ (2) \Rightarrow \ (c-a) = -(b-c) \Rightarrow \ a=b \ \ $but$ \ a,b \ $are distinct, a contradiction! )
Ah yes my bad. Right idea and pretty close to being done, but we can have a pair of the k's being -1 instead of all of them having to be 1.
