dan964
what
Re: HSC 2014 4U Marathon - Advanced Level
q14 and 16 are both out of 16 not 15
q14 and 16 are both out of 16 not 15
Last edited:
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
Here is a good question:
 \ $be the average of all positive divisors of positive integer$ \ n \\ \\ $Show that$ \ f(n) \geq \sqrt{n} )
yep although there is an easier way of doing it using demouivre's theorem.Is this the solution for 14ai?
=RHS
Nice proof!is the number of positive divisors of
, and note that these divisors must occur in pairs
and thus
is even.
Define the divisors to be
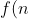 \geq \sqrt{n})
I think this is only valid if all m prime factors are distinct.Nice proof!
Here is mine:

Yea it is, my badI think this is only valid if all m prime factors are distinct.
read the question "absolutely every n" is the key phrase. Sure it may work for non-prime p for certain n, but for all.By the way, I think the "only if" statement in 15bii) is not true. Counterexample: p=561.
I did read the question.read the question "absolutely every n" is the key phrase. Sure it may work for non-prime p for certain n, but for all.
If you think I am bluffing, Q15b is a reworking of Fermat's theorem.
2047 is another. Have you tried with base 3 (n=3), or base 5 (n=5) as well.
part (iii) proves that for n=2, some numbers other than primes work e.g. 2047
the proof to Q15(b)(ii) comes from part (i) which is an interesting property of Pascal's triangle that can be proved quite easily.
Errata Q14 (A)(ii) use part (i)
One other interesting thing about Primes (p>5), and testing for them. (a quick way)
1. You can test all numbers up to the squareroot
2. Check whether divisible by 2,3 and 5.
3. You can easily check whether the last digit is a 2,4,5,6,8 or 0
4. You can also only divide by numbers that are of the form 6m +1 or 6m - 1 (since all primes occur either side of these numbers), so that removes all multiples of 3 as well.
here is an interesting extension (for if p/n is not an integer) for all prime numbers if I write (p-1) 1s (then a zero) in that base it is also divisible. (Provided n/= p). Hence 1,111,110 (and therefore 111,111) is divisible by 7, and 111,111,111,1110 and therefore (111,111,111,111) is divisible by 13.
What is this post in reply to? I still think n^561-n is divisible by 561 for every positive integer n, despite 561 not being prime. This is in contradiction with the "only if" part of your question. (By the way, I got this number because it is the lowest Carmichael number, and I checked the non-coprime moduli myself.)Use a similar method to Q15(b) with n = 3 but this time prove by contradiction it doesn't work.
Done
I never said induction in p, that would be insane/impossible because p goes over the primes. I meant induction in n, which is straightforward becauseProve by induction for n rather than p is a bit easier.
FLT is not IFF, glittergal is right.read the question "absolutely every n" is the key phrase. Sure it may work for non-prime p for certain n, but for all.
If you think I am bluffing, Q15b is a reworking of Fermat's theorem.
Wait, so what is the full question then? I don't see how this fits in anywhere that makes sense.fine then a small edit:
Restriction: Provided that (6m+1), (12m+1), (18m+1) are not prime factors; if p is composite.
Advanced

