Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
HINT: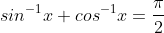
There is just try my question and then do his its geniusI doubt there's a solution for Ekman's question, although I might be wrong cause I didn't spend enough time on it
HINT:
Last edited:


