-
Looking for HSC notes and resources? Check out our Notes & Resources page
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2015 MX2 Integration Marathon (archive) (2 Viewers)
- Thread starter Sy123
- Start date
- Status
- Not open for further replies.
Ekman
Well-Known Member
- Joined
- Oct 23, 2014
- Messages
- 1,612
- Gender
- Male
- HSC
- 2015
Last edited:
porcupinetree
not actually a porcupine
- Joined
- Dec 12, 2014
- Messages
- 661
- Gender
- Male
- HSC
- 2015
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
A relation that just involves In, Jn, Kn would not be a recurrence relation. It would have to involves smaller values of n.Question: http://imgur.com/r357wc1
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon

dan964
what
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Paradoxica
-insert title here-
Re: MX2 2015 Integration Marathon

The rest can be easily done using the standard log and arctan integral forms.

EDIT: hmmmm... Wolfram Alpha says I'm wrong..... Where are the mistakes?
Wrong, you let u^15 = xIm thinking let u=x^15

The rest can be easily done using the standard log and arctan integral forms.

EDIT: hmmmm... Wolfram Alpha says I'm wrong..... Where are the mistakes?
Last edited:
Re: MX2 2015 Integration Marathon
I can't see your pictures.Wrong, you let u^15 = x

The rest can be easily done using the standard log and arctan integral forms.

EDIT: hmmmm... Wolfram Alpha says I'm wrong..... Where are the mistakes?
kawaiipotato
Well-Known Member
- Joined
- Apr 28, 2015
- Messages
- 462
- Gender
- Undisclosed
- HSC
- 2015
Re: MX2 2015 Integration Marathon
I tried using the substituion
x = u^(15/4)
Which will then lead to u^4/(1+u^3) requiring long division and then a fractional decomposition. But then it didnt give me an arctan?
I tried using the substituion
x = u^(15/4)
Which will then lead to u^4/(1+u^3) requiring long division and then a fractional decomposition. But then it didnt give me an arctan?
Paradoxica
-insert title here-
Re: MX2 2015 Integration Marathon
Evaluate

For a similar but easier problem, evaluate

Evaluate
For a similar but easier problem, evaluate
Last edited:
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
I think they are both equal to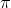 .
.
For the sum one:
\\ \\= \lim_{N\rightarrow\infty}\sum_{|n|\leq N}(\arctan(n+1/2)-\arctan(n-1/2)\right))\\ \\= \lim_{N\rightarrow\infty}(\arctan(N+1/2)-\arctan(-(N+1/2)))\\ \\=\pi.)
Typing integral one up now.
I think they are both equal to
For the sum one:
Typing integral one up now.
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
\cdot\arctan\left(\frac{1}{x^2+3/4}\right)\, dx\\ \\ = \int_{-R}^R \frac{4x^2\, dx}{1+(x^2+3/4)^2}\, dx\\ \\ = \int_{-R}^R \left(\frac{x}{1+(x-1/2)^2}-\frac{x}{1+(x+1/2)^2}\right)\, dx\\ \\ = \int_{-R-1/2}^{R-1/2} \frac{x+1/2}{1+x^2}\, dx - \int_{-R+1/2}^{R+1/2} \frac{x-1/2}{1+x^2}\, dx \\ \\ = \int_{-R+1/2}^{R-1/2}\frac{dx}{1+x^2}-2\int_{R-1/2}^{R+1/2}\frac{dx}{1+x^2}\\ \\ \rightarrow \pi.)
(Since the first term is just 2*arctan(R-1/2) and the second has size bounded by 2/(1+(R-1/2)^2), which tends to zero.)
(Since the first term is just 2*arctan(R-1/2) and the second has size bounded by 2/(1+(R-1/2)^2), which tends to zero.)
Last edited:
Paradoxica
-insert title here-
Re: MX2 2015 Integration Marathon
Hm, interesting approach. I thought you would have split the arctangent directly as you did in the summation. Whatever runs through the mind faster I guess...
(In an exam you should of course write these improper integrals as the limit of integrals from -T to T, to justify things like splitting and recombining them, and the use of integration by parts. Some of the integrals as written in the above working don't actually exist as improper integrals over the full real line.)
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
Is it a consequential difference? Either way we get an arctan integral, which we perform by integrating by parts.Hm, interesting approach. I thought you would have split the arctangent directly as you did in the summation. Whatever runs through the mind faster I guess...
glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: MX2 2015 Integration Marathon
I guess it can be made quicker.
-\arctan(x-1/2)\, dx = 2\int_R^{R+1/2}\arctan(x)\, dx.\\ \\ $So $2\arctan(R)\leq I_R \leq 2\arctan(R+1/2)\\ \\ $from which the squeeze law completes the proof.$)
I guess it can be made quicker.
- Status
- Not open for further replies.



