Re: HSC 2015 4U Marathon - Advanced Level
I'm a bit rusty, but let's give this a go.
Consider each student's report in terms of an
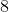
-element, ordered string of
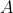
's and
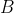
's. We know we must satisfy both the stated conditions, that
)
no two strings are the same, and
)
there cannot be a string that beats another in a cohort of reports. We examine the second condition, and note that in such a cohort of reports, we select any two strings and must find that there is an

and a

correspondence between the first and the second string respectively. This is the minimum difference (
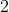
grades) required to meet
)
and equalize the two strings.
Given a fixed, arbitrary number of
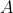
's and
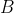
's, we generate different strings to meet
)
, and find that in the process we satisfy
)
since we only have
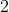
possible elements, and hence must switch an
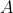
and a
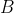
in moving between unique strings.
In that case we have

reports in a satisfactory cohort, where the integer

.
One could argue that moving on to a different number of
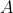
's and
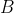
's (changing

) satisfies
)
by giving another combinatoric set of reports with totally different strings.
Consider one of these new strings, however. First, we find a string in the original cohort with the greatest number of identical grades. Then, we note that the difference would be either a number of

correspondences or a number of

correspondences. This is because the new string will have more/less of one grade than the original string when we are trying to match the two.
Such bias means one of these two strings would beat the other. Therefore, an exhaustive cohort of satisfactory reports must have a fixed number of
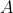
's and
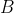
's, and be of the above-stated combinatoric form. We know from the (ninth) row Pascal's triangle that to maximise this, we choose
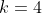
. Hence

=

.
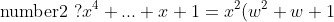 \\ RHS= x^2 (x^2 +2 +\frac{1}{x^2} +x + \frac{1}{x}+1) \\= x^4 +2x^2 +1 +x^3 +x +x^2 \\ =x^4 +x^3 +3x^2 +x +1 ?... )
