glittergal96
Active Member
- Joined
- Jul 25, 2014
- Messages
- 418
- Gender
- Female
- HSC
- 2014
Re: 2015 permutation X2 marathon
A recursive formula is easy enough.
Picture the n people as black beads, numbered 1 through n, and the n committees as white beads, numbered 1 through n.
How many ways can we create a finite collection of bracelets, where the beads on each bracelet alternate in colour, and each bracelet has at least four beads total?
Each way of doing this corresponds to a unique way of putting people into committees. (adjacency <=> committee membership).
Now if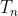 is the number of ways of doing this with n beads of each colour, we have:
is the number of ways of doing this with n beads of each colour, we have:

where is the number of ways of making a single bracelet with n beads of each colour.
is the number of ways of making a single bracelet with n beads of each colour.
This formula comes from considering the size of the bracelet containing the alphabetically first person, choosing the other n-1 black beads and n white beads for this bracelet, forming a bracelet from these beads, and forming a finite collection of bracelets with the remaining n-k beads of each colour.
Of course, it is also possible that all beads are in a single bracelet, which is where the last term comes from.
Since!}{2}) , our expression simplifies to:
, our expression simplifies to:
!}{2}\sum_{k=0}^{n-2}\frac{T_k}{(k!)^2} \quad (n\geq 2)})
(We set by convention.)
by convention.)
A recursive formula is easy enough.
Picture the n people as black beads, numbered 1 through n, and the n committees as white beads, numbered 1 through n.
How many ways can we create a finite collection of bracelets, where the beads on each bracelet alternate in colour, and each bracelet has at least four beads total?
Each way of doing this corresponds to a unique way of putting people into committees. (adjacency <=> committee membership).
Now if
where
This formula comes from considering the size of the bracelet containing the alphabetically first person, choosing the other n-1 black beads and n white beads for this bracelet, forming a bracelet from these beads, and forming a finite collection of bracelets with the remaining n-k beads of each colour.
Of course, it is also possible that all beads are in a single bracelet, which is where the last term comes from.
Since
(We set
Last edited:
