davidgoes4wce
Well-Known Member
Re: HSC 2016 3U Marathon
makes it :
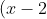^2=4a [(2x-7)+1] )
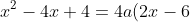 )
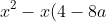+(4-24a)=0 )
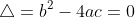
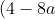^2-4(4-24a)=0 )
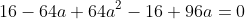
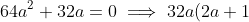=0 )
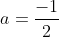
a cannot be 0 in this case because it must be a quadratic form.
So you say let y=2x-7 (which I didn't get at the time)The parabola takes the form (x-2)^2=4a(y+1)
A wolfram alpha approach: Sub y=2x-7 in and simplify the expression
Take the quadratic discriminant, set it equal to 0 and take your value for a
makes it :
a cannot be 0 in this case because it must be a quadratic form.


