Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2016 MX2 Complex Numbers Marathon (archive) (1 Viewer)
- Thread starter math man
- Start date
- Status
- Not open for further replies.
parad0xica
Active Member
- Joined
- Mar 24, 2016
- Messages
- 204
- Gender
- Male
- HSC
- N/A
Re: HSC 2016 Complex Numbers Marathon
 is bisected
is bisected
Source: http://www.coolmath.com/reference/kites
Whoops, I meant that the chordA kites diagonals do not bisect each other
Source: http://www.coolmath.com/reference/kites
Re: HSC 2016 Complex Numbers Marathon
Another problem is the centre of the circle is not the midpoint of the chord, it's impossible. I'll give you a hint to solve it really easily in a few seconds. The intersection of the tangents is the point w so if you let OW be the complex number w you can sub z=w and then use the fact w lies on u1 + u2
Another problem is the centre of the circle is not the midpoint of the chord, it's impossible. I'll give you a hint to solve it really easily in a few seconds. The intersection of the tangents is the point w so if you let OW be the complex number w you can sub z=w and then use the fact w lies on u1 + u2
parad0xica
Active Member
- Joined
- Mar 24, 2016
- Messages
- 204
- Gender
- Male
- HSC
- N/A
Re: HSC 2016 Complex Numbers Marathon
I can't think of anything for this besides w = c(u1 +u2) where is c is real...Another problem is the centre of the circle is not the midpoint of the chord, it's impossible. I'll give you a hint to solve it really easily in a few seconds. The intersection of the tangents is the point w so if you let OW be the complex number w you can sub z=w and then use the fact w lies on u1 + u2
Re: HSC 2016 Complex Numbers Marathon
The best approach to these harder questions is to use the answer and think given what you have what you need to prove, since OW is diameter prove |w|=2/|u1+u2| and a more advanced method is play with that result and you get prove |w(u1+u2)|=2 which looks familiar if you add those two equations I said. I call this the Greek method as you play with the answer and put it in a form that is easier to prove
The best approach to these harder questions is to use the answer and think given what you have what you need to prove, since OW is diameter prove |w|=2/|u1+u2| and a more advanced method is play with that result and you get prove |w(u1+u2)|=2 which looks familiar if you add those two equations I said. I call this the Greek method as you play with the answer and put it in a form that is easier to prove
KingOfActing
lukewarm mess
Re: HSC 2016 Complex Numbers Marathon
EDIT: I'm just gonna rewrite it without quoting the formula's to see how difficult it is
Edit 2: I rewrote it above, not actually that difficult. More geometrical than complex numbers, but it's still valid.
The best approach to these harder questions is to use the answer and think given what you have what you need to prove, since OW is diameter prove |w|=2/|u1+u2| and a more advanced method is play with that result and you get prove |w(u1+u2)|=2 which looks familiar if you add those two equations I said. I call this the Greek method as you play with the answer and put it in a form that is easier to prove
Edit 2: I rewrote it above, not actually that difficult. More geometrical than complex numbers, but it's still valid.
Last edited:
parad0xica
Active Member
- Joined
- Mar 24, 2016
- Messages
- 204
- Gender
- Male
- HSC
- N/A
Re: HSC 2016 Complex Numbers Marathon
 + w(\overline{u_1}+\overline{u_2}) =4)
Taking reals
)= 2)
Now finding imaginary
 - w(\overline{u_1}+\overline{u_2}) = c(\overline{u_1+u_2})(u_1+u_2) - c(u_1+u_2)(\overline{u_1+u_2}) = 0)
) = 0)
 = 2 + 0i)
 |= 2)
Of course,

How's this?
__________________________
What you call Greek method is heuristically known as working backwards and thanks for the hints btw
AddingThe best approach to these harder questions is to use the answer and think given what you have what you need to prove, since OW is diameter prove |w|=2/|u1+u2| and a more advanced method is play with that result and you get prove |w(u1+u2)|=2 which looks familiar if you add those two equations I said. I call this the Greek method as you play with the answer and put it in a form that is easier to prove
Taking reals
Now finding imaginary
Of course,
How's this?
__________________________
What you call Greek method is heuristically known as working backwards and thanks for the hints btw
Last edited:
KingOfActing
lukewarm mess
Re: HSC 2016 Complex Numbers Marathon
Don't you have to prove that OW is the diameter?Adding
Taking reals
Now finding imaginary
 - w(\overline{u_1}+\overline{u_2}) = c(\overline{u_1+u_2})(u_1+u_2) - c(u_1+u_2)(\overline{u_1+u_2}) = 0)
Of course,
How's this?
__________________________
What you call Greek method is heuristically known as working backwards and thanks for the hints btw
Re: HSC 2016 Complex Numbers Marathon
Yes. Luckily it's pretty quick to prove. Angle OU1W is 90 degrees so by converse of 'angle in a semicircle', OW is the diameter.Don't you have to prove that OW is the diameter?
parad0xica
Active Member
- Joined
- Mar 24, 2016
- Messages
- 204
- Gender
- Male
- HSC
- N/A
Re: HSC 2016 Complex Numbers Marathon
Angle WU1O is 90 degrees by tangent-radius theorem, hence OW is diameter.
Beaten by the swift puɐɹפǝʇuI
My bad, I forgot this was for the user, wu345.Don't you have to prove that OW is the diameter?
Angle WU1O is 90 degrees by tangent-radius theorem, hence OW is diameter.
Beaten by the swift puɐɹפǝʇuI
KingOfActing
lukewarm mess
Re: HSC 2016 Complex Numbers Marathon
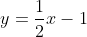 with the domain restricted to
with the domain restricted to 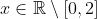 which can be shown algebraically by using arg(z) - arg(w) = arg(z/w)
which can be shown algebraically by using arg(z) - arg(w) = arg(z/w)
Alternatively, the geometrical interpretation is that the angle between the points P(0,-1), Z(x,y) and Q(2,0) is 0.
It is the lineNEW
Q: sketch arg(z-2)=arg(z+i)
Alternatively, the geometrical interpretation is that the angle between the points P(0,-1), Z(x,y) and Q(2,0) is 0.
KingOfActing
lukewarm mess
Re: HSC 2016 Complex Numbers Marathon

Re: HSC 2016 Complex Numbers Marathon
+\tan^{-1}(x+y)+\tan^{-1}\frac{2x}{x^2-y^2-1}=\pi)
and hence if x=2 and y=1 then
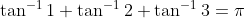
Better still, prove that
and hence if x=2 and y=1 then
KingOfActing
lukewarm mess
Re: HSC 2016 Complex Numbers Marathon

(c-d) + (a-d)(b-c)\right|\\&=|ac-ad-bc+bd+ab-bd-ac+dc|\\&=|a(b-d) - c(b-d)|\\&=|a-c||b-d| \\&= AC \cdot BD\\\text{Q.E.D.}\end{align*})
(c-d)\right) = \arg\left( (a-d)(b-c)\right)$. This can be simplified down to $\arg(a-b) - \arg(c-b) - \pi = -\left(\arg(c-d) -\arg(a-d)\right) \Longleftrightarrow \angle ABC + \angle CDA = \pi$. Hence equality is achieved if and only if the quadrilateral is cyclic.$)
By using complex numbers, show that for a quadrilateral ABCD, we have:
AB.CD + AD.BC >= AC.BD.
When does equality occur?
parad0xica
Active Member
- Joined
- Mar 24, 2016
- Messages
- 204
- Gender
- Male
- HSC
- N/A
Re: HSC 2016 Complex Numbers Marathon
(1+i)(1+2i)(1+3i) = -10
arg((1+i)(1+2i)(1+3i)) = arg(-10 )
arg(1+i)+ arg(1+2i)+arg(1+3i) = \pi
arctan(1) + arctan(2) + arctan(3) = \pi
EDIT: added "spoilers"
Highlight below to see answer:
(1+i)(1+2i)(1+3i) = -10
arg((1+i)(1+2i)(1+3i)) = arg(-10 )
arg(1+i)+ arg(1+2i)+arg(1+3i) = \pi
arctan(1) + arctan(2) + arctan(3) = \pi
EDIT: added "spoilers"
Last edited:
Paradoxica
-insert title here-
Re: HSC 2016 Complex Numbers Marathon
I need them. My life force is running dry...
Actually, I was wondering, do you have any more magical trigonometric identities?Better still, prove that
and hence if x=2 and y=1 then
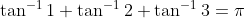
I need them. My life force is running dry...
- Status
- Not open for further replies.
