Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
HSC 2017 MX2 Integration Marathon (archive) (1 Viewer)
- Thread starter leehuan
- Start date
- Status
- Not open for further replies.
Re: HSC 4U Integration Marathon 2017
<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;\frac{sinx&space;-&space;cosx}{(sinx+cosx)\sqrt{sinxcosx&space;+&space;sin^2xcos^2x}}" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;\frac{sinx&space;-&space;cosx}{(sinx+cosx)\sqrt{sinxcosx&space;+&space;sin^2xcos^2x}}" title="\int \frac{sinx - cosx}{(sinx+cosx)\sqrt{sinxcosx + sin^2xcos^2x}}" /></a>
<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;\frac{sinx&space;-&space;cosx}{(sinx+cosx)\sqrt{sinxcosx&space;+&space;sin^2xcos^2x}}" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;\frac{sinx&space;-&space;cosx}{(sinx+cosx)\sqrt{sinxcosx&space;+&space;sin^2xcos^2x}}" title="\int \frac{sinx - cosx}{(sinx+cosx)\sqrt{sinxcosx + sin^2xcos^2x}}" /></a>
Re: HSC 4U Integration Marathon 2017
<a href="https://www.codecogs.com/eqnedit.php?latex=\inline&space;\int&space;\frac{1}{x^2-3x+2}&space;=\int&space;\frac{1}{(x-1)(x-2)}&space;=&space;\int&space;\frac{1}{x-2}&space;-&space;\int&space;\frac{1}{x-1}&space;=&space;\ln&space;(x-2)&space;-&space;\ln&space;(x-1)&space;+C" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\inline&space;\int&space;\frac{1}{x^2-3x+2}&space;=\int&space;\frac{1}{(x-1)(x-2)}&space;=&space;\int&space;\frac{1}{x-2}&space;-&space;\int&space;\frac{1}{x-1}&space;=&space;\ln&space;(x-2)&space;-&space;\ln&space;(x-1)&space;+C" title="\int \frac{1}{x^2-3x+2} =\int \frac{1}{(x-1)(x-2)} = \int \frac{1}{x-2} - \int \frac{1}{x-1} = \ln (x-2) - \ln (x-1) +C" /></a>
Re: HSC 4U Integration Marathon 2017
Also, a way to do this is note that arcsin(root(0))=0, and so this can be evaluated using the integral from 0 to a of a function of x = ab - the integral from 0 to b of the inverse function of x, where f(a)=b. I had to type this like I just did sorry haha.
Re: HSC 4U Integration Marathon 2017
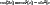 and
and 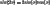 to simplify the inside the integrals to get
to simplify the inside the integrals to get
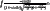
use substitution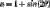
then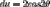
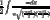
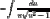
let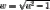
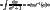 constant
constant
From the you can see the integrals is tan inverse of \sqrt{u^2-1}
We can back track to find it in terms of theta
you can rearrange<a href="https://www.codecogs.com/eqnedit.php?latex=\int&space;\frac{sinx&space;-&space;cosx}{(sinx+cosx)\sqrt{sinxcosx&space;+&space;sin^2xcos^ 2x}}" target="_blank"><img src="https://latex.codecogs.com/gif.latex?\int&space;\frac{sinx&space;-&space;cosx}{(sinx+cosx)\sqrt{sinxcosx&space;+&space;sin^2xcos^ 2x}}" title="\int \frac{sinx - cosx}{(sinx+cosx)\sqrt{sinxcosx + sin^2xcos^2x}}" /></a>
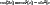 and
and 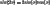 to simplify the inside the integrals to get
to simplify the inside the integrals to get 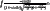
use substitution
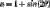
then
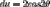
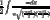
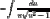
let
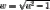
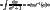 constant
constantFrom the you can see the integrals is tan inverse of \sqrt{u^2-1}
We can back track to find it in terms of theta
Attachments
-
1.5 KB Views: 60
Last edited:
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 4U Integration Marathon 2017
Learn Latex pls
Learn Latex pls
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Re: HSC 4U Integration Marathon 2017

leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Last edited:
Paradoxica
-insert title here-
Re: HSC 4U Integration Marathon 2017
Why that reaction haha? Is there some story behind this integral?smh...
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Re: HSC 4U Integration Marathon 2017

Seen it before a bit too many timesWhy that reaction haha? Is there some story behind this integral?
Paradoxica
-insert title here-
Re: HSC 4U Integration Marathon 2017
don't scare off the children
Re: HSC 4U Integration Marathon 2017
Checked it on wolfram so it's all good.
http://imgur.com/a/LQn6t
Checked it on wolfram so it's all good.
- Status
- Not open for further replies.