i dont understand graphs (1 Viewer)

[bleakarcher]

in working, wen determining critical points. they simply state as y approaches a, dy/dx approaches b. how can they just simply state this? where does it come from

 

[hup]

give an example

 

[bleakarcher]

when try to graph y=x^(1/3)
the cambridge textbook solution:
dy/dx=(1/3)x^(-2/3)
as x approaches 0 from the right, dy/dx approaches infinity
as x approaches 0 from the left, dy/dx approaches negative infinity
hence dy/dx is not defined at x=0
hence there is a vertical tangent at x=0
wtf?
can somone please explain

 

[ohexploitable]

lol m8



it's just the inverse fn of y=x^3

 

[bleakarcher]

wat lol?

 

[bleakarcher]

i know that it is. but wat is all this shit about critical points. in harder questionz, how would we determine this where it is less obvious?

 

[bleakarcher]

hup, where did u disappear to...?

 

[hup]

if you graph
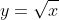
and you see at x = 0
those kind of points are considered critical points, because the function 'ends' there
any 'sharp' points ( like cusps) or single points are critical points
more egs

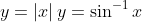
the sharp point on y = absx and the points for x = 1,-1 on sin inverse
these are considered critical points because if you were asked to draw a tangent at that point, you cant draw one, because the tangent could pass through at any steepness and still pass through the point

algebraically you can see


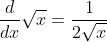
and as x goes to 0, the bottom goes to 0 so dy/dx goes to infinity
whenever the gradient approaches infinity in that way it means the gradient of the tangent is undefined at that point
and you can see from the graph why

for the approaching part you just substitute values close to the suspected critical points
for your question
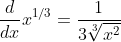
and you see that as bottom approaches 0 it will have some critical point
so you test x=0.00001 and x=-0.0000001 to see from both sides etc

 

[bleakarcher]

also as x approaches 0 from the left doesnt dy/dx approach positive infinity coz it u take the tangent at some point when x=a and then the tangent at another point when x=b, where a is less than b which is less than 0, u will find that the tangent at x=b is steeper. isnt dy/dx therefore approaching positive infinity instead of negative. i know there is some fallacy here but i just want my mind clear.

 

[hup]

idk what you are trying to say

 

[bleakarcher]

can u explain the behaviour of the graph y=x^(1/3) as x approaches 0 from the left thanks

 

[hup]

can u explain the behaviour of the graph y=x^(1/3) as x approaches 0 from the left thanks

 

[bleakarcher]

thank you. i was reading this one textbook which told me as x approaches 0 from the left, dy/dx approaches negative infinity