Okay so the idea for the well-known Heaviside cover-up method goes like this
Suppose you have something like
\left(2x+1\right)}})
What happens is that you split this into partial fractions which will give us
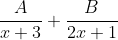
. Intuitively you would cover one of the factors
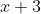
or
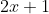
with your finger and then say oh let x=-3 or let x=
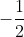
.
At this point, you might be wondering why we make such statements. First and foremost it will allow us to find the values for A and B and also the backbone of the Heaviside cover-up method goes like this
From
\left(2x+1\right)}}=\frac{A}{x+3}+\frac{B}{2x+1})
we multiply by
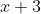
or
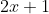
on both sides so that we get a constant which is either A or B and if you think about it a constant is your best friend for integration because they will stay the same regardless of the value you have for x.
To show my proof what is actually happening is that from
\left(2x+1\right)}}=\frac{A}{x+3}+\frac{B}{2x+1})
multiplying by
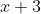
will give us
}}=A+\frac{B\left(x+3\right)}{2x+1})
. Do you see the constant A, well now we will say let x=-3 because you want
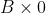
for the fraction because 0 divided by anything on the denominator is still 0. As a result of this our working will be easy because just sub in x=-3 on the LHS and you should get
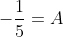
. Repeat this process and you will have
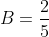
.
Now you you remember when I said that we can do this over here "Intuitively you would cover one of the factors
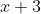
or
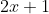
with your finger and then say oh let
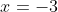
or let
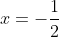
." The reason why we could do that is because of the backbone of the Heaviside cover-up method as I explained earlier from the previous two paragraph.
I hope this helps you understand how the cover-up rule works and also why it works so well. If you still have any difficulties feel free to reply on this post and someone here will explain it more concisely for you.

