induction q (1 Viewer)
- Thread starter mr.habibbi
- Start date
33^n+1 - 16^n+1 - 28^n+1 + 11^n+1View attachment 32200
do this since ur so smart
=16(33^n-16^n-28^n+11^n) + 17(33^n-28^n) + 5(28^n-11^n)
= not bothered to type out
= 85k
Life'sHard
Well-Known Member
- Joined
- May 24, 2021
- Messages
- 1,102
- Gender
- Male
- HSC
- 2021
- Uni Grad
- 2025
Lmao33^n+1 - 16^n+1 - 28^n+1 + 11^n+1
=16(33^n-16^n-28^n+11^n) + 17(33^n-28^n) + 5(28^n-11^n)
= not bothered to type out
= 85k
1, 2 skip a few 99, 10033^n+1 - 16^n+1 - 28^n+1 + 11^n+1
=16(33^n-16^n-28^n+11^n) + 17(33^n-28^n) + 5(28^n-11^n)
= not bothered to type out
= 85k
x^n-y^n factorisation where u pull out something to make 851, 2 skip a few 99, 100
ye still dont see itx^n-y^n factorisation where u pull out something to make 85
Eagle Mum
Well-Known Member
- Joined
- Nov 9, 2020
- Messages
- 561
- Gender
- Female
- HSC
- N/A
x^n-y^n factorisation where u pull out something to make 85
x^n-y^n is divisible by (x-y) There’s a different induction proof for this.ye still dont see it
Therefore, 17(33^n-28^n) + 5(28^n-11^n) = 17*(33-28)*N1 + 5(28-11)*N2 = 17*5N1 + 5*17N2 = 85(N1 + N2)
In an induction proof, the first component of the algebraic expression is assumed to be divisible by 85.
Last edited:
geniusx^n-y^n is divisible by (x-y) There’s a different induction proof for this.
Therefore, 17(33^n-28^n) + 5(28^n-11^n) = 17*(33-28)*N1 + 5(28-11)*N2 = 17*5N1 + 5*17N2 = 85(N1 + N2)
In an induction proof, the first component of the algebraic expression is assumed to be divisible by 85.
A similar approach...
Result (A)
\left(x^{n-1} + x^{n-2}y + x^{n-3}y^2 + ... + y^{n-1}\right) \quad \text{for positive integers $n$} \\ \\ \textbf{Proof:} \qquad \text{RHS}\ &= (x - y)\left(x^{n-1} + x^{n-2}y + x^{n-3}y^2 + ... + y^{n-1}\right) \\ &= x\left(x^{n-1} + x^{n-2}y + x^{n-3}y^2 + ... + y^{n-1}\right) - y\left(x^{n-1} + x^{n-2}y + x^{n-3}y^2 + ... + y^{n-1}\right) \\ &= x^n + x^{n-1}y + x^{n-2}y^2 + ... + xy^{n-1} - \left(x^{n-1}y + x^{n-2}y^2 + x^{n-3}y^3 + ... + y^n\right) \\ &= x^n + \left(x^{n-1}y - x^{n-1}y\right) + \left(x^{n-2}y^2 - x^{n-2}y^2\right) + ... + \left(xy^{n-1} - xy^{n-1}\right) - y^n \\ &= x^n - y^n \\ &= \text{LHS} \end{align*})
It follows that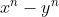 is divisible by
is divisible by 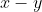 for all positive integers
for all positive integers 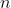 .
.
Corollaries of Result (A)
) is also divisible by 17.
is also divisible by 17.
HAHS Proof 1
) is also divisible by 5.
is also divisible by 5.
Having proven the given result is divisible by both 17 and 5, and since these numbers are coprime, it immediately follows that the statement is also divisible by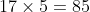 .
.
I didn't notice the proof of divisibility by 5, however, and proceeded instead to prove that the statement is divisible by 5 another way:
Re-casting the induction proof approach:
It follows from above that I seek to prove that:
 - 16\left(16^n\right)}{17} \\ &= \cfrac{33\left(17M_n + 16^n\right) - 16 \times 16^n}{17} \qquad \qquad \text{as $M_n =\cfrac{X_n}{17} = \cfrac{33^n - 16^n}{17}$} \\ &= \cfrac{17\times 33M_n + 16^n(33 - 16)}{17} \\ &= 33M_n + 16^n \end{align*})
And, by similar reasoning,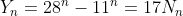 where
where 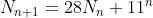 .
.
Note further that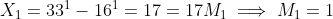 and that
and that 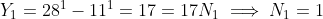 .
.
\ \text{is divisible by five for all positive integers $n$)
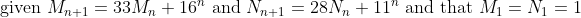
The core part of the proof by induction will have as the induction hypothesis that
 = 5P \quad \text{for some positive integer $P$})
and the working will establish that
 \\ &= 17\left[5\times M_k + 28\left(M_k - N_k\right) + 16^k - 11^k\right] \\ &= 17\left(5\times M_k + 28\times 5P + 16^k - 11^k\right) \qquad \qquad \text{after using the induction hypothesis} \\ &= 17\left(5\times M_k + 28\times 5P + 5L\right) \qquad \qquad \text{noting that $16^k - 11^k = 5L$, for some integer $L$, using result (a)} \\ &= 17 \times 5\left(M_k + 28P + L\right) \end{align*})
NOTES:
Result (A)
It follows that
Corollaries of Result (A)
is divisible by
.
is divisible by
.
HAHS Proof 1
is divisible by
.
is divisible by
.
Having proven the given result is divisible by both 17 and 5, and since these numbers are coprime, it immediately follows that the statement is also divisible by
I didn't notice the proof of divisibility by 5, however, and proceeded instead to prove that the statement is divisible by 5 another way:
Re-casting the induction proof approach:
It follows from above that I seek to prove that:
- Defining
and
, I seek that
is divisible by 85.
- It has been established that
is divisible by 17, and that I only need
to be divisible by 5.
And, by similar reasoning,
Note further that
The core part of the proof by induction will have as the induction hypothesis that
and the working will establish that
NOTES:
- As an induction problem, this is too hard to be reasonable as a test of MX2 content.
- The assumption that this is an induction problem is just that - an assumption. This question illustrates a comment that I have made before, that the Proof section of the new syllabus offers opportunities to ask very difficult questions and the extent of this will be explored over years to come.
- Splitting
into
in the induction part uses the same idea / approach as is key in @idkkdi's very concise proof above
- The question could just have easily asked for a proof that the result is divisible by 170, as this is obviously follows once the divisibility by 85 is established.
A similar approach...
Result (A)
It follows thatis divisible by
for all positive integers
.
Corollaries of Result (A)
Thus,
is divisible by
.
is divisible by
.
is also divisible by 17.
HAHS Proof 1
Thus,
is divisible by
.
is divisible by
.
is also divisible by 5.
Having proven the given result is divisible by both 17 and 5, and since these numbers are coprime, it immediately follows that the statement is also divisible by.
I didn't notice the proof of divisibility by 5, however, and proceeded instead to prove that the statement is divisible by 5 another way:
Re-casting the induction proof approach:
It follows from above that I seek to prove that:
- Defining
and
, I seek that
is divisible by 85.
- It has been established that
is divisible by 17, and that I only need
to be divisible by 5.
And, by similar reasoning,where
.
Note further thatand that
.
The core part of the proof by induction will have as the induction hypothesis that
and the working will establish that
NOTES:
- As an induction problem, this is too hard to be reasonable as a test of MX2 content.
- The assumption that this is an induction problem is just that - an assumption. This question illustrates a comment that I have made before, that the Proof section of the new syllabus offers opportunities to ask very difficult questions and the extent of this will be explored over years to come.
- Splitting
into
in the induction part uses the same idea / approach as is key in @idkkdi's very concise proof above
- The question could just have easily asked for a proof that the result is divisible by 170, as this is obviously follows once the divisibility by 85 is established.

nvm, was being dumb.
Last edited:
stupid_girl
Active Member
- Joined
- Dec 6, 2009
- Messages
- 221
- Gender
- Undisclosed
- HSC
- N/A
This is essentially a watered-down version of another question that I had seen before.View attachment 32200
do this since ur so smart
Prove that 2903^n – 803^n – 464^n + 261^n is divisible by 1897 for any positive integers.
This kind of problem can be solved by number theory in a much more elegant way. It is just not worthwhile to restrict yourself to MI and spend ages on some messy algebra like this.

Last edited:
can we get an admin to change her name?This is essentially a watered-down version of another question that I had seen before.
Prove that 2903^n – 803^n – 464^n + 261^n is divisible by 1897 for any positive integers.
This kind of problem can be solved by number theory in a much more elegant way. It is just not worthwhile to restrict yourself to MI and spend ages on some messy algebra like this.
View attachment 32214
Are you sure?just something to add,
View attachment 32213
result A only holds true for n, where n is odd.
probably need to take either two cases, or a more general proof.
Certainly the factorisation of
However, I am not seeing any flaw in the reasoning that I have used that falisfies the result for the case where
What do you think is wrong with my proof / reasoning?
was mixing it up with x^n+y^n which doesn't work for even.Are you sure?
Certainly the factorisation ofonly works for odd
(as then
, allowing the above factorisation to be used).
However, I am not seeing any flaw in the reasoning that I have used that falisfies the result for the case whereis even and the result is certainly true for:
What do you think is wrong with my proof / reasoning?
Which question do you mean?Check out James Ruse 2018 Paper. I swear there was something similar!
