Integral of 0 (1 Viewer)
- Thread starter asianese
- Start date
the indefinite integral of 0 is a constant - think when you derive the equations of projectile motion in regards to horizontal motion
the area under the curve idea can be applied with the idea of a definite integral, except you're finding the area of the curve bound by the x-axis and the line y=0 (which is also the x-axis), so therefore your "area" will always be 0
the area under the curve idea can be applied with the idea of a definite integral, except you're finding the area of the curve bound by the x-axis and the line y=0 (which is also the x-axis), so therefore your "area" will always be 0
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Well when you find the area underneath the curve when you integrate it and apply the Fundemental Theorem of Calculus:
i.e
 \ dx=F(b)-F(a) \\ F'(x)=f(x) )
When you do this, the +C's cancel out when you subtract them. And because the C's cancel out, people dont put them in for simplicity's sake (or maybe a deeper mathematical reason)
For example: Find the area underneath the curve of y=x^2 from x=1 to x=0:
-(0+C) = \frac{1}{3} )
In a similar vein:

Well thats how Ive seen it anyway.
i.e
When you do this, the +C's cancel out when you subtract them. And because the C's cancel out, people dont put them in for simplicity's sake (or maybe a deeper mathematical reason)
For example: Find the area underneath the curve of y=x^2 from x=1 to x=0:
In a similar vein:
Well thats how Ive seen it anyway.
iSplicer
Well-Known Member
+1, well articulated.Well when you find the area underneath the curve when you integrate it and apply the Fundemental Theorem of Calculus:
i.e
When you do this, the +C's cancel out when you subtract them.
For example: Find the area underneath the curve of y=x^2 from x=1 to x=0:
In a similar vein:
Well thats how Ive seen it anyway.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
I'm a little confused as to what you mean here, but what guarantee is there that the C's are the same, such that they cancel out?Well when you find the area underneath the curve when you integrate it and apply the Fundemental Theorem of Calculus:
i.e
When you do this, the +C's cancel out when you subtract them. And because the C's cancel out, people dont put them in for simplicity's sake (or maybe a deeper mathematical reason)
For example: Find the area underneath the curve of y=x^2 from x=1 to x=0:
In a similar vein:
Well thats how Ive seen it anyway.
iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,374
- Gender
- Male
- HSC
- 2013
Precisely what I was wondering.I'm a little confused as to what you mean here, but what guarantee is there that the C's are the same, such that they cancel out?
lolcakes52
Member
- Joined
- Oct 31, 2011
- Messages
- 286
- Gender
- Undisclosed
- HSC
- 2012
Yes, what sy123 said is what we do when we find the area usually. We just skip the step because its trivial.
D94
New Member
- Joined
- Oct 5, 2011
- Messages
- 4,423
- Gender
- Male
- HSC
- N/A
Well, the C is the constant of integration. The derivative of x2+4 is the same as the derivative of x2+7, but the integral of 2x is not necessarily x2+4 or x2+7. The C is sort of a placeholder for the antiderivative constant - we don't know it until we put in limits. So in the case where we bound the integrand, there is no constant of integration as we know it, but rather a specific integral solution.Also, Ive read from a number of sources that say that it is that reason that we dont write Cs when doing a definite integral. But if its wrong its wrong I guess...
I don't see why you added the + C in your original reply.
- Joined
- Feb 16, 2005
- Messages
- 8,402
- Gender
- Male
- HSC
- 2006
The C's must be the same, otherwise the definite integral will always contain an arbitrary constant. From the fundamental theorem of calculus:I'm a little confused as to what you mean here, but what guarantee is there that the C's are the same, such that they cancel out?
Notice that the first term and the second term of the RHS use the same primitive function F(x), therefore it must be the same constant. For example, suppose we have this situation with differently labelled constants:
then
and
Since a and b only appear in the first term, and we're referring to the same function F, the constants C1 and C2 must clearly be equal.
The constant is there to demonstrate that the primitive function is not unique. However, when we refer to F(x) we are implictly referring to a 'specific' primitive function with C taking some fixed value and not varying. Hence, in the fundamental theorem of calculus, the C's must be fixed otherwise it behaves like a variable.
Last edited:
RealiseNothing
what is that?It is Cowpea
But you're still integrating the same function (ie f(x)), you just use different x values which since it's a constant won't change them, so they have to be equal don't they?I'm a little confused as to what you mean here, but what guarantee is there that the C's are the same, such that they cancel out?
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Ohhhh right I understand what he is saying now. I thought he was saying this:
 = f(x) \\\\ $Therefore integrating both sides with respect to $ x $ yields:$ \\\\ F(x) + C = g(x) + C \\\\ $Therefore $ F(x) = g(x).)
Which is of course not necessarily the case since as I said before (in response to an incorrect interpretation anyway haha), there's no guarantee that the constants are the same.
This is because if the derivative of F(x) is f(x), it does NOT mean that the integral of f(x) is F(x).
Which is of course not necessarily the case since as I said before (in response to an incorrect interpretation anyway haha), there's no guarantee that the constants are the same.
This is because if the derivative of F(x) is f(x), it does NOT mean that the integral of f(x) is F(x).
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
I don't think the concept of 'taking out the 0' works. Consider the following scenario then:Guys, I think you are overcomplicating things...
Simply,
In the case of indefinite integrals,

Using a Cauchy Principal Value will of course give us 0 as the final answer (not quite happy about having to use it though), but then you run into problems with divergent indefinite integrals, say:
Also, your last line doesn't quite work in this case because suppose k were some arbitrary constant, then by your working out, we should have:
asianese
Σ
- Joined
- Sep 20, 2010
- Messages
- 2,225
- Gender
- Undisclosed
- HSC
- 2012
Well the reason why I raised the question was because in an actuaries careers talk the guy asked a question:
 And he was trying to get at +C, which would solve the anomaly of 0 = -1, but he said that
And he was trying to get at +C, which would solve the anomaly of 0 = -1, but he said that  but yeah I imagined the curve
but yeah I imagined the curve 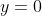 and it's 'infinite 0' area..
and it's 'infinite 0' area..
Last edited:
RealiseNothing
what is that?It is Cowpea
The integrals aren't right.Well the reason why I raised the question was because in an actuaries careers talk the guy asked a question:
And he was trying to get at +C, which would solve the anomaly of 0 = -1, but he said that
but yeah I imagined the curve
and it's 'infinite 0' area..
Uhh, usually when I evaluate something like
