kendricklamarlover101
Member
- Joined
- Oct 22, 2023
- Messages
- 79
- Gender
- Male
- HSC
- 2024
can someone check if my working is correct i got this integral from spivak's calculus
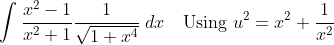
dx)
dx)
(x^2+1)}{x^3} \; dx)
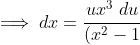(x^2+1)})
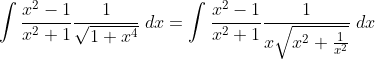
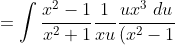(x^2+1)} = \int \frac{x^2}{\left(x^2 +1\right)^2} \; du)
^2} \; du = \int \frac{1}{u^2 + 2} \; du)
 = \frac{1}{\sqrt{2}} \arctan \left( \frac{\sqrt{x^4+1}}{x\sqrt{2}} \right) + C)
also are there any alternative methods than this substitution?
also are there any alternative methods than this substitution?


