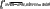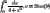<a href="http://www.codecogs.com/eqnedit.php?latex=\int_{0}^{2} \frac{dx}{1 @plus; x^2} ~,~x=2tan\theta \\\\ \frac{1}{4}\int_{\frac{\pi}{4}}^{0} \frac{2sec^2\theta }{1 @plus; tan^2\theta}~d\theta ~,~ 1 @plus;tan^2\theta \Rightarrow sec^2\theta \\\\ = \frac{1}{4}\int_{0}^{\frac{\pi}{4}} 2~d\theta \\\\ = \frac{1}{2}\left [ \theta\right ]_{0}^{\frac{\pi}{4}} \\\\ = \frac{1}{2}(\frac{\pi}{4}) = \frac{\pi}{8} \approx \frac{1}{3}" target="_blank"><img src="http://latex.codecogs.com/gif.latex?\int_{0}^{2} \frac{dx}{1 + x^2} ~,~x=2tan\theta \\\\ \frac{1}{4}\int_{\frac{\pi}{4}}^{0} \frac{2sec^2\theta }{1 + tan^2\theta}~d\theta ~,~ 1 +tan^2\theta \Rightarrow sec^2\theta \\\\ = \frac{1}{4}\int_{0}^{\frac{\pi}{4}} 2~d\theta \\\\ = \frac{1}{2}\left [ \theta\right ]_{0}^{\frac{\pi}{4}} \\\\ = \frac{1}{2}(\frac{\pi}{4}) = \frac{\pi}{8} \approx \frac{1}{3}" title="\int_{0}^{2} \frac{dx}{1 + x^2} ~,~x=2tan\theta \\\\ \frac{1}{4}\int_{\frac{\pi}{4}}^{0} \frac{2sec^2\theta }{1 + tan^2\theta}~d\theta ~,~ 1 +tan^2\theta \Rightarrow sec^2\theta \\\\ = \frac{1}{4}\int_{0}^{\frac{\pi}{4}} 2~d\theta \\\\ = \frac{1}{2}\left [ \theta\right ]_{0}^{\frac{\pi}{4}} \\\\ = \frac{1}{2}(\frac{\pi}{4}) = \frac{\pi}{8} \approx \frac{1}{3}" /></a>