Timothy.Siu
Prophet 9
n=/= 0 means n cant equal 0No. that was the full question.
btw can you explain a bit more, what does " n=/=0" mean?
n=/= 0 means n cant equal 0No. that was the full question.
btw can you explain a bit more, what does " n=/=0" mean?
if you see the working first part, towards the end, you can see n in the demominator.No. that was the full question.
btw can you explain a bit more, what does " n=/=0" mean?
when doing the working you get to:No. that was the full question.
btw can you explain a bit more, what does " n=/=0" mean?
Yea, true. Thanksif you see the working first part, towards the end, you can see n in the demominator.
Thus n cannot be 0.
Drongoski, you forgot to change the limits as you made the substitution...Great effort study-freak!
Per Timothu.Siu's suggestion, for U(0):
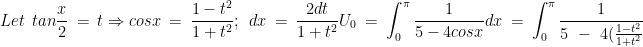}\times \frac{2dt}{1+t^{2}}\\ \\ =\ \ \int_{0}^{\pi }\frac{2}{1+9t^{2}}dt\ \ =\ \ \frac{2}{3}tan^{-1}(3t)]^{\pi }_{0}\ \ =\ \ \left [ \frac{2}{3}tan^{-1}(3tan\frac{x}{2}) \right ]^{\pi }_{0}\\ \\ =\ \ \frac{2}{3}[tan^{-1}(3\ tan\frac{\pi }{2})\ -\ tan^{-1}(3tan\ 0)]\ \ =\ \ \frac{2}{3}[\frac{\pi }{2}\ -\ 0]\ \ =\ \ \frac{\pi }{3})
yes.If n=0 isn't it true that U (n) becomes U (0) = S 1/ (5-4cosx) dx [ from x =0 to x= pi] ?
Drongoski, you forgot to change the limits as you made the substitution...
What can be done, is to find:
using a t-substitution and let a approach
So your integral becomes:
As a approaches, this expression approaches

i dont think he forgot, although i guess the working out is incorrect with the limits.Drongoski, you forgot to change the limits as you made the substitution...
What can be done, is to find:
using a t-substitution and let a approach
So your integral becomes:
As a approaches, this expression approaches

You know that for y = tan-1x, as x approaches infinity, y approaches π/2.How did you know this?
I don't think this works because I remember doing one integration problem in two different methods and one method gave answers like Ctan^(-1) (ktan(pi/2)) where C and k were integral, C,k>1 while the other method gave out an actual real number like pi/3 or something like that.You know that for y = tan-1x, as x approaches infinity, y approaches π/2.
Now with tan-1(3tan a/2)
as a-->π, tan a/2 --> ∞
and
3tan a/2 --> ∞
hence tan-1(3tan a/2) --> π/2
so (2/3) tan-1(3tan a/2) --> π/3
I'm pretty sure that it should work in this case. In Ctan^(-1) (ktan(pi/2)), the answer (in the limit) would be Cpi/2...The method I posted above was the evaluation step of the t-substitution.I don't think this works because I remember doing one integration problem in two different methods and one method gave answers like Ctan^(-1) (ktan(pi/2)) where C and k were integral, C,k>1 while the other method gave out an actual real number like pi/3 or something like that.
When I tried using your method to evaluate the answer from the 1st method, I failed to produce the same answer as the one I obtained using the 2nd method (which was the t method). I was sure that there was no error with other calculations and I also had others to check it. I don't remember the question so I can't post it though.
Even if the integral seems to approach (pi/3) when x approaches pi as you've stated above, pi/3 still can't be regarded as an answer can it?Drongoski, you forgot to change the limits as you made the substitution...
What can be done, is to find:
using a t-substitution and let a approach
So your integral becomes:
As a approaches, this expression approaches

It is covered in the first session of mathematics for Engineering as well.Thanks for your explanation.
btw how did you get to know all these things such as the "improper integrals"?
