Intermediate Value Theorem Proof Q (1 Viewer)

mreditor16 · Apr 12, 2015

Anyone willing to help out with part c)? thankssss

VBN2470 · Apr 12, 2015

mreditor16 said:
Anyone willing to help out with part c)? thankssss

From the top of my head, for (i) I can think of $\frac{x}{x^2+1}$ and for (ii) I can think of $\frac{-1}{1+x^2}$ . For (iii), you will need to consider the case where the you split the interval into $(-\infty, M_1), [M_1, M_2]$ and $(M_2, \infty)$ and apply the Extreme Value Theorem + definition of a limit. Perhaps someone like InteGrand can actually give a more detailed solution, since I cbf typing it up on LaTeX.

InteGrand · Apr 12, 2015

mreditor16 said:
Anyone willing to help out with part c)? thankssss

I think you'll be able to get the essence of the proof from here (slightly different Q):

VBN2470 said:
NEW QUESTION:

$$ Given that $f$ is a continuous function on $\mathbb{R}$ such that $f(0)=0$ and $\lim_{x\to\infty} f(x)=0$, prove that $f$ attains a maximum on $[0, \infty)$.$

Don't know if this was the right place to post this q.

InteGrand said:
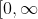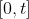
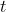
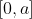
Since is continuous on $[0,\infty)$ , it continuous on $[0,t]$ for any positive real number $t$ . If $f(x)$ is never positive, then clearly attains a maximum (0) at x = 0. So assume is positive somewhere in the interval $[0,a]$ , where $a$ is some positive real number.

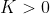
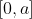
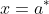
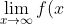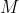
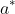
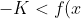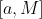
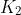
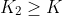
By the Extreme Value Theorem, attains a maximum value $K>0$ on $[0,a]$ , say at $x=a^*$ . Since $\lim_{x\to \infty}f(x)=0$ , it means that for all $x$ greater than some positive number $M$ (which must be greater than $a^*$ ), we will have $-K<f(x)<K$ . Now consider the interval $[a, M]$ . By the Extreme Value Theorem, attains a maximum $K_2$ on here. 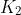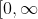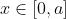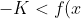If $K_2 \geq K$ , then attains the maximum value $K_2$ on the interval $[0,\infty)$ (since $f(x)\leq K \leq K_2$ for all $x \in [0,a]$ and $-K<f(x)<K\leq K_2$ for all $x\in [M,\infty)$ ). 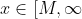Otherwise (i.e. 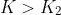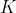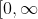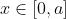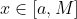$K>K_2$ ), attains the maximum value $K$ on $[0,\infty)$ , since $f(x)\leq K$ for all $x \in [0,a]$ , $f(x)\leq K_2 < K$ for all $x\in [a,M]$ , and $f(x)<K$ for all $x\in [M,\infty)$ . 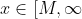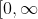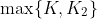In either case, indeed attains a maximum on $[0,\infty)$ (the maximum being $\max\{K,K_2\}$ ).

(The represents f, the font messed up a bit.)

InteGrand · Apr 12, 2015

mreditor16 said:
anyone willing to help out with part c)? Thankssss

PROOF OUTLINE:

Let $f(\xi)=\Xi >0$ .

By definition of limits to infinity, there exist $M>N$ such that $|f(x)-0|<\Xi$ whenever $x>M$ and whenever $x<N$ . So $\xi \in [N,M]$ , and:

(1) $f(x)<\Xi \text{ }\forall x \in (-\infty, N)$

(2) $f(x)<\Xi \text{ }\forall x\in(M,\infty)$ .

By the extreme value theorem (since f is continuous), $f$ attains a maximum value $K$ on $[N,M]$ .

Since $f(x)=\Xi >0$ when $x= \xi \in [N,M]$ , this maximum $K$ satisfies $K\geq \Xi$ . (3)

(1), (2) and (3) imply that f attains a maximum value on $\mathbb{R}$ , namely $f_\text{max.}=K$ .

Intermediate Value Theorem Proof Q (1 Viewer)

mreditor16

Well-Known Member

VBN2470

Well-Known Member

InteGrand

Well-Known Member

InteGrand

Well-Known Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)