Q1a: You want to use the idea: if you have a*b = 0, then either a=0 or b=0. So in this case, you can say that either
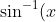 = 0)
or
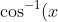 = 0)
. You can then try to solve each of these, and my preferred way would be to use a graph. You should get x = 0 and 1.
Q1b: This one is a lot trickier. One way is to try to convert them all to
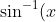)
(of course, you can also convert them to
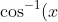)
). So you would want to make use of the identity
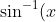 + \cos^{-1} (x) = \frac{\pi}{2})
. Then you'll end up with an equation with just
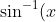)
, so for convenience, you would want to let
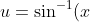)
. After that, if you put everything to one side, you should end up with a quadratic equation, and if you solve it, you should get two values of u which are:
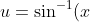 = \frac{\pi}{4} \pm \frac{1}{2} \sqrt{\frac{\pi^2}{4} + 4} \approx 2.06, -0.49)
Now to solve for x, you'll realise that one of these values is invalid due to the domain of the inverse sine function. Let me know if that's enough for you to work with.
Q1c: It's unclear what the question is. I'm assuming it is:
 + 2 \cos^{-1} (x-1) = \frac{\pi}{2})
(There is an extra x after the cosine so I'll ignore that.) What you can do is move the 2nd term to the right hand side, and then take the sine of both sides. You'll end up getting
\right) = \sin \left( \frac{\pi}{2} - 2 \cos^{-1} (x-1) \right))
Lucky the inverse sine and sine 'cancel each other out', and on the right hand side you can make use of the fact that sin(pi/2 - x) = cos(x), You can then use one of the double angle formulas, and if you simplify everything you should end up with a quadratic equation with solutions 0 and 3/2. But whenever you're dealing with inverse functions, always make sure to substitute it back to the original equation (you can always accidentally introduce new solutions). It will turn out that x=0 is not a solution, so the only solution is x = 3/2.
