ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 unit (2 Viewers)
- Thread starter Examine
- Start date
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
So the points A B C and D need to touch the circumference?
See in this picture how points C and D are on the same side of the interval AB.
Now if angle ACB=angle ADB, it means that ABDC is cyclic.
Because if you remember, angles on the circumference subtended by the same are equal.
Conversely, if two angles subtended by the same chord (or arc) are equal, the four points must lie on the circumference of a circle. (i.e Concyclic)
iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,374
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un

Very basic exam question: State why BEDC is a cyclic quadrilateral.
In this example, because two angles subtended by the same interval are equal, those four points are cyclic.
Its just another way to prove points are cyclic.
If the angles were equal, then yes those four points would be on the circumference of a circle.So the points A B C and D need to touch the circumference?

Very basic exam question: State why BEDC is a cyclic quadrilateral.
In this example, because two angles subtended by the same interval are equal, those four points are cyclic.
Its just another way to prove points are cyclic.
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
The exterior angle and the opposite angle rules?Examine, do you know all the methods of proving points are cyclic/form a cyclic quadrilateral?
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Does that mean that in this situation it is still concyclic, yet the circle it makes is positioned at another place (for all points to touch the circumference)?
So let's say that we had the same situation as outlined, though in the diagram one of the angle points did not touch the circumference, yet is the same angle as the other one which does.If the angles were equal, then yes those four points would be on the circumference of a circle.

Very basic exam question: State why BEDC is a cyclic quadrilateral.
In this example, because two angles subtended by the same interval are equal, those four points are cyclic.
Its just another way to prove points are cyclic.
Does that mean that in this situation it is still concyclic, yet the circle it makes is positioned at another place (for all points to touch the circumference)?
Solution
BoS Revolutionary
- Joined
- Aug 3, 2012
- Messages
- 120
- Gender
- Undisclosed
- HSC
- N/A
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
If you have proved that 4 points are cyclic and one of them does not visually lie on the given circle, this means that it lies on another circle ie One that goes through those 4 points. I might not be too clear here, but I hope you get the right message.
I think I get what you're trying to say.So let's say that we had the same situation as outlined, though in the diagram one of the angle points did not touch the circumference, yet is the same angle as the other one which does.
Does that mean that in this situation it is still concyclic, yet the circle it makes is positioned at another place (for all points to touch the circumference)?
If you have proved that 4 points are cyclic and one of them does not visually lie on the given circle, this means that it lies on another circle ie One that goes through those 4 points. I might not be too clear here, but I hope you get the right message.
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Oh yes I get it thanks.I think I get what you're trying to say.
If you have proved that 4 points are cyclic and one of them does not visually lie on the given circle, this means that it lies on another circle ie One that goes through those 4 points. I might not be too clear here, but I hope you get the right message.
iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,374
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
If the points are on the circumference, then they are equal (if subtended by same or equal arc), and conversely, assume no circle is drawn, if two points subtend equal angles from a line, then they all lie on a circumference of a circle.
Im not fully sure what you're saying, can you draw a diagram.So let's say that we had the same situation as outlined, though in the diagram one of the angle points did not touch the circumference, yet is the same angle as the other one which does.
Does that mean that in this situation it is still concyclic, yet the circle it makes is positioned at another place (for all points to touch the circumference)?
If the points are on the circumference, then they are equal (if subtended by same or equal arc), and conversely, assume no circle is drawn, if two points subtend equal angles from a line, then they all lie on a circumference of a circle.
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
For something like this, if you were to apply the theorem it would mean that they are concyclic right? (even though one point does not touch the circumference). Does this mean that you can generate a circle which would touch all 4 points?

For something like this, if you were to apply the theorem it would mean that they are concyclic right? (even though one point does not touch the circumference). Does this mean that you can generate a circle which would touch all 4 points?

Solution
BoS Revolutionary
- Joined
- Aug 3, 2012
- Messages
- 120
- Gender
- Undisclosed
- HSC
- N/A
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Yes - you proved that A,B,C,D are cyclic points that lie on a circle ie One that goes through A,B,C,DFor something like this, if you were to apply the theorem it would mean that they are concyclic right? (even though one point does not touch the circumference). Does this mean that you can generate a circle which would touch all 4 points?

iBibah
Well-Known Member
- Joined
- Jun 13, 2012
- Messages
- 1,374
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Yes they are concyclic, except they lie on a different circle to the one you have there.For something like this, if you were to apply the theorem it would mean that they are concyclic right? (even though one point does not touch the circumference). Does this mean that you can generate a circle which would touch all 4 points?

RealiseNothing
what is that?It is Cowpea
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Through any 3 points (that are not collinear), there is ONLY ONE unique circle that can be made. Hence if the quadrilateral is concyclic, then the 4th point must lie on the circle. In the diagram you posted, the point 'c' MUST lie on the circle given, if not then the angles are not equal.
This is impossible.For something like this, if you were to apply the theorem it would mean that they are concyclic right? (even though one point does not touch the circumference). Does this mean that you can generate a circle which would touch all 4 points?

Through any 3 points (that are not collinear), there is ONLY ONE unique circle that can be made. Hence if the quadrilateral is concyclic, then the 4th point must lie on the circle. In the diagram you posted, the point 'c' MUST lie on the circle given, if not then the angles are not equal.
RealiseNothing
what is that?It is Cowpea
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
His diagram is impossible.
Yes - you proved that A,B,C,D are cyclic points that lie on a circle ie One that goes through A,B,C,D
They can only lie on one circle, and one circle only.Yes they are concyclic, except they lie on a different circle to the one you have there.
His diagram is impossible.
Carrotsticks
Retired
- Joined
- Jun 29, 2009
- Messages
- 9,494
- Gender
- Undisclosed
- HSC
- N/A
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
Yep, it's because the theorem (angle subtended same chord same side blah blah) is an IFF definition.They can only lie on one circle, and one circle only.
His diagram is impossible.
Sy123
This too shall pass
- Joined
- Nov 6, 2011
- Messages
- 3,730
- Gender
- Male
- HSC
- 2013
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
So what we need to do, to find the focal length, is to get the equation into the form:
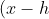^2=4a(y-k) )
Where a is our focal length:
^2=x^2+6x+(\frac{x^2}{2}) \\ y+4=(x+3)^2 \\ \\ \therefore a=\frac{1}{4} )
Therefore our focal length is 0.25
You just need to use completing the square to get it into that focal length form
So what we need to do, to find the focal length, is to get the equation into the form:
Where a is our focal length:
Therefore our focal length is 0.25
You just need to use completing the square to get it into that focal length form
Re: ITT we help examine to get 85 in his Maths extension 1 yearlies so he can do 4 un
 )
)
I have reached that form, though I don't understand how you reached a=1/4. (Seems like what I thought was how to do it was wrongSo what we need to do, to find the focal length, is to get the equation into the form:
Where a is our focal length:
Therefore our focal length is 0.25
You just need to use completing the square to get it into that focal length form
