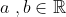locus of (a+bz) (1 Viewer)

juantheron · Apr 7, 2012

if $\mid z \mid= 2$ , then find the locus of complex number $(a + bz)$

where $a\;,b\in \mathbb{R}$

juantheron · Apr 7, 2012

$\hspace{-16} $Here $\bf{\mid z \mid = 2}$ and Here We have to find the value of $\bf{(a+bz)}$\\\\\\ $\bf{\mid a+bz\mid \leq \mid a \mid+\mid b \mid .\mid z \mid\Leftrightarrow \mid a+bz\mid \leq a+2b\;\;.\; a,b\in \mathbb{R}}$\\\\\\ $\bf{\mid a+bz \mid^2 \leq (a+2b)^2}$\\\\\\ Let $\bf{z=x+iy}$. Then $\bf{\mid a+b(x+iy)\mid^2 \leq (a+2b)^2}$\\\\\\ $\bf{(a+bx)^2+(by)^2\leq a^2+4b^2+4ab}$\\\\\\ $\bf{a^2+b^2x^2+2abx+b^2y^2\leq a^2+4b^2+4ab}$\\\\\\ $\bf{b^2x^2+b^2y^2+2abx-4b^2-4ab\leq 0}$\\\\\\ $\bf{x^2+y^2+2.\frac{a}{b}.x-4-4.\frac{a}{b}\leq 0}$\\\\\\ $\bf{\left(x+\frac{a}{b}\right)^2+y^2\leq \left(\frac{a}{b}\right)^2+\frac{4a}{b}+4}$\\\\\\ $\bf{\left(x+\frac{a}{b}\right)^2+y^2\leq \left(\frac{a}{b}+2\right)^2}$$

Is is Right Or Not

lolcakes52 · Apr 7, 2012

This is a lot of working for a relatively easy question. The locus of z is a circle centre 0,0 and radius 2. The locus of bz is a circle centre 0,0 with radius of 2b. The value of a shifts this circle in the real axis. So we have the locus of a+bz with radius 2b and centre at (-a,0) its late so im not sure but im pretty sure thats right.

barbernator · Apr 7, 2012

the locus will not be an area, it will be a curve/line. There should not be any inequalities involved.

math man · Apr 7, 2012

the locus is $\frac{(x-a)^{2}}{b^{2}} + \frac{y^{2}}{b^{2}} = 4$

To deduce this we let $z=x_{1} + iy_{1}$ subject to $x_{1}^{2} + y_{1}^{2} = 4$
for our question $a + bz$ we want to find the locus of this point so we let $x= Re(a+bz)=a+bx_1$
and we let $y=Im(a+bz)=by_{1}$
then you just make our parameters the subject square both sides and plug the condition in and you get the above answer

juantheron · Apr 8, 2012

Thanks Friends got it

locus of (a+bz) (1 Viewer)

juantheron

Active Member

juantheron

Active Member

lolcakes52

Member

barbernator

Active Member

math man

Member

juantheron

Active Member

Users Who Are Viewing This Thread (Users: 0, Guests: 1)