Let y = e^x
Take the log of both sides and we have
ln(y) = ln(e^x)
Using the log law ln(m^n) = nln(m),
ln(y) = xln(e)
Notice that ln(e) = 1 (or using the log law
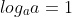
for all real a > 0)
ln(y) = x
If you understand this, then you can try to figure out a quite way of converting y = e^x into ln(y) = x (consider the movements and transformations of 'e' and 'ln')