Last edited:
Make a Difference – Donate to Bored of Studies!
Students helping students, join us in improving Bored of Studies by donating and supporting future students!
- Home
- Forums
- Tertiary Education
- Universities
- University of New South Wales
- Australian School of Business
MATH1251 Questions HELP (1 Viewer)
- Thread starter 1008
- Start date
Paradoxica
-insert title here-
Not only is that answer wrong, that is a horrible abuse of notation (making the index variable the same as the defining subscript.)
Drsoccerball
Well-Known Member
- Joined
- May 28, 2014
- Messages
- 3,647
- Gender
- Undisclosed
- HSC
- 2015
Paradoxica is more salty than the Pacific Ocean...Not only is that answer wrong, that is a horrible abuse of notation (making the index variable the same as the defining subscript.)
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Actually whilst maybe not as strongly felt, I did think the same way he didParadoxica is more salty than the Pacific Ocean...
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Parts a), b) and c) are purely for reference

Here's a proof to part d) (I) also for the sake of reference
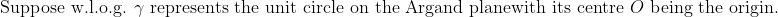
)
\\ \implies AB \le AX \, \forall X \in \gamma)
Q: How would you go about (II)? I want to try proof by contradiction but I'm not sure how to go about anything

Here's a proof to part d) (I) also for the sake of reference
Q: How would you go about (II)? I want to try proof by contradiction but I'm not sure how to go about anything
Parts a), b) and c) are purely for reference

Here's a proof to part d) (I) also for the sake of reference
Q: How would you go about (II)? I want to try proof by contradiction but I'm not sure how to go about anything
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Interpreting the MATLAB output: It's just the RREF of the matrix representation augmented with the identity.
i.e. the RREF of)

How is the output supposed to help me do c)?
Because I thought the image would just be
i.e. the RREF of

How is the output supposed to help me do c)?
Because I thought the image would just be
Last edited:
The right-hand matrix's columns (which started off being the standard basis vectors) are all leading columns if placed next to the reduced row-echelon form of A. Hence none of the standard basis vectors are in the image of T.Interpreting the MATLAB output: It's just the RREF of the matrix representation augmented with the identity.
i.e. the RREF of

How is the output supposed to help me do c)?
Because I thought the image would just be
(It's like augmenting A with a single vector to solve a system of equations, except we augmented with four vectors (the four standard basis vectors), which is like looking at solving four separate systems of equations.)
Paradoxica
-insert title here-
It is one variable... Maybe differentiate it as the unit vector?Are there some subtleties that we need to consider here or is this actually just as easy to do in R?

seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
The answer here mildly depends on:Are there some subtleties that we need to consider here or is this actually just as easy to do in R?

a) your definition of the exponential function.
b) whether theta ranges over R or C. (and hence whether the differentiation refers to differentiation with respect to a complex variable or a real variable)
c) which facts along the lines of the chain rule you know and can assume.
leehuan
Well-Known Member
- Joined
- May 31, 2014
- Messages
- 5,794
- Gender
- Male
- HSC
- 2015
Hmm. I was picturing theta to be a complex variable, because I didn't want to consider a real variable with complex coefficients or something.The answer here mildly depends on:
a) your definition of the exponential function.
b) whether theta ranges over R or C. (and hence whether the differentiation refers to differentiation with respect to a complex variable or a real variable)
c) which facts along the lines of the chain rule you know and can assume.
Which definitions of the exponential function should I choose from?
(I actually forgot what definition we used in high school. Possibly the limit of (1+x/n)^n?)
Also chain rule: All I know is dy/dx = dy/du . du/dx, over R (not sure if result holds over C)
seanieg89
Well-Known Member
- Joined
- Aug 8, 2006
- Messages
- 2,653
- Gender
- Male
- HSC
- 2007
In high school you don't define the exponential function per se, you define the real number e as the unique real number a such that a^x has slope 1 at the origin, and then you work with e^x from there. This is a terribly nonrigorous, because high school mathematics does not rigorously define the reals, let alone what it means to raise the real number a to the real power x, etc. It is best to largely forget high school definitions of things, and just recall your high school experience in computing things like integrals etc.Hmm. I was picturing theta to be a complex variable, because I didn't want to consider a real variable with complex coefficients or something.
Which definitions of the exponential function should I choose from?
(I actually forgot what definition we used in high school. Possibly the limit of (1+x/n)^n?)
Also chain rule: All I know is dy/dx = dy/du . du/dx, over R (not sure if result holds over C)
The most common and cleanest definition of the exponential for use in higher math is the power series
Now since complex power series are complex differentiable in the interior of their disk of convergence (*) (the derivative is obtained by differentiating the power series "term-by-term"), and the function z -> iz is complex differentiable everywhere, we can apply the (complex) chain rule to draw the desired conclusion.
The complex chain rule is that if f:X->Y and g:Y->Z are complex differentiable, then (gof) is complex differentiable with derivative g'(f(z))f'(z). Since you were not sure that this result held true, you should try to prove it if you go about this method of solution to the original question.
If you wanted to avoid using the chain rule, you could alternatively use the fact that the derivative of a power series is given by differentiating term by term. Writing exp(iz) as a power series, differentiate term by term to explicitly show that we arrive at i*exp(iz).
Note:
If you are unfamiliar with (*), the result that power series can be differentiated term by term in the interior of their disk of convergence, you should prove this too.

